Câu hỏi/bài tập:

Cho tam giác nhọn ABC cân tại đỉnh A. Đường tròn đường kính BC cắt các cạnh AB, AC của tam giác ABC lần lượt tại F và E.
a) Cho BE cắt CF tại H. Chứng minh rằng AH vuông góc với BC.
b) Chứng minh rằng EF song song với BC.

a) Chứng minh \(BE \bot AC,CF \bot AB\), suy ra H là trực tâm tam giác ABC nên AH vuông góc với BC.
Advertisements (Quảng cáo)
b) Chứng minh \(\widehat {EFC} = \widehat {EBC}\), \(\widehat {EBC} = {90^o} - \widehat {ECB} = {90^o} - \widehat {FBC} = \widehat {FCB}\) nên \(\widehat {EFC} = \widehat {FCB}\), suy ra EF//BC.

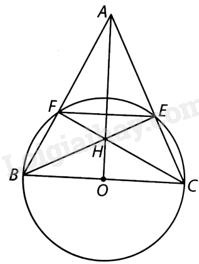
a) Gọi O là đường tròn đường kính BC. Vì \(\widehat {BEC}\) và \(\widehat {CFB}\) là các góc nội tiếp của (O) cùng chắn nửa đường tròn nên \(\widehat {BEC} = \widehat {CFB} = {90^o}\). Suy ra \(BE \bot AC,CF \bot AB\). Do đó H là trực tâm của tam giác ABC. Vì vậy AH vuông góc với BC.
b) Vì \(\widehat {EFC}\) và \(\widehat {EBC}\) là các góc nội tiếp của (O) cùng chắn nên \(\widehat {EFC} = \widehat {EBC}\) (1)
Mặt khác, tam giác ABC cân tại A và các tam giác BCF, CBE lần lượt vuông tại F và E nên \(\widehat {EBC} = {90^o} - \widehat {ECB} = {90^o} - \widehat {FBC} = \widehat {FCB}\). (2)
Từ (1) và (2) ta suy ra \(\widehat {EFC} = \widehat {FCB}\). Do đó EF//BC (hai góc ở vị trí so le trong)
