
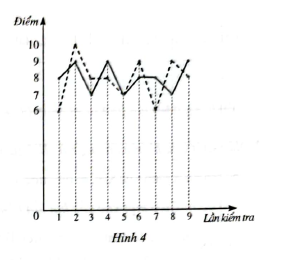
Biểu đồ đoạn thẳng ở Hình 4 cho biết kết quả thi Ngoại ngữ ở CLB của Dũng (đường nét liền) và Hoàng (đường nét đứt đậm) qua 9 lần kiểm tra
a) Viết mẫu số liệu thống kê kết quả thi ngoại ngữ của Dũng và Hoàng nhận được từ biểu đồ ở Hình 4
b) Tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu đó
c) Tính phương sai và độ lệch chuẩn của hai mẫu số liệu đó. Cho biết kết quả thi của bạn nào ổn định hơn?

+ Liệt kê các giá trị trong biểu đồ và sắp xếp các số liệu theo thứ tự không giảm
+ Tìm khoảng biến thiên theo công thức\(R = {x_n} - {x_1}\) với số cao nhất và thấp nhất lần lượt \({x_n},{x_1}\)
+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} - {Q_1}\)
Bước 1: Sắp xếp các số liệu theo thứ tự không giảm.
Bước 2: Tính cỡ mẫu \(n\), tìm tứ phân vị thứ hai \({Q_2}\)(chính là trung vị của mẫu).
Bước 3: Tìm tứ phân vị thứ nhất: là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Bước 4: Tìm tứ phân vị thứ ba: là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
+ Tìm phương sai theo công thức \({S^2} = \frac{1}{n}\left( {{n_1}{x_1}^2 + {n_2}{x_2}^2 + ... + {n_k}{x_k}^2} \right) - {\overline x ^2}\) và độ lệch chuẩn \(S = \sqrt {{S^2}} \)

a)
+ Mẫu số liệu kết quả thi của bạn Dũng là: 8; 9; 7; 9; 7; 8; 8; 7; 9.
+ Mẫu số liệu kết quả thi của bạn Hoàng là: 6; 10; 8; 8; 7; 9; 6; 9; 8.
b)
- Sắp xếp mẫu số liệu theo thứ tự tăng dần
Mẫu số liệu kết quả thi của bạn Dũng là: 7; 7; 7; 8; 8; 8; 9; 9; 9 (1)
Advertisements (Quảng cáo)
Mẫu số liệu kết quả thi của bạn Hoàng là: 6; 6; 7; 8; 8; 8; 9; 9; 10 (2)
- Khoảng biến thiên:
+ Mẫu số liệu (1): Số cao nhất và thấp nhất lần lượt là 9 và 7 do đó khoảng biến thiên của dãy số liệu là: \(R = 9 - 7 = 2\)
+ Mẫu số liệu (2): Số cao nhất và thấp nhất lần lượt là 10 và 6 do đó khoảng biến thiên của dãy số liệu là: \(R = 10 - 6 = 4\)
- Mẫu số liệu (1):
+ Vì \(n = 9\) là số lẻ nên tứ phân vị thứ hai là: \({Q_2} = 8\) là tứ phân vị
+ Tứ phân vị thứ nhất là trung vị của 4 số đầu tiên của mẫu số liệu: \({Q_1} = \left( {7 + 7} \right):2 = 7\)
+ Tứ phân vị thứ ba là trung vị của 4 số cuối của mẫu số liệu: \({Q_3} = \left( {9 + 9} \right):2 = 9\)
+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} - {Q_1} = 9 - 7 = 2\)
- Mẫu số liệu (2):
+ Vì \(n = 9\) là số lẻ nên tứ phân vị thứ hai là: \({Q_2} = 8\) là tứ phân vị
+ Tứ phân vị thứ nhất là trung vị của 4 số đầu tiên của mẫu số liệu: \({Q_1} = \left( {6 + 7} \right):2 = 6,5\)
+ Tứ phân vị thứ ba là trung vị của 4 số cuối của mẫu số liệu: \({Q_3} = \left( {9 + 9} \right):2 = 9\)
+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} - {Q_1} = 9 - 6,5 = 2,5\)
c)
- Mẫu số liệu (1):
+ Số trung bình cộng: \(\overline x = \frac{{3.7 + 3.8 + 3.9}}{9} = 8\)
+ Phương sai: \({S^2} = \frac{1}{9}({3.7^2} + {3.8^2} + {3.9^2}) - {8^2} = \frac{2}{3}\)
+ Độ lệch chuẩn: \(S = \sqrt {{S^2}} = \sqrt {\frac{2}{3}} = \frac{{\sqrt 6 }}{3}\)
- Mẫu số liệu (2):
+ Số trung bình cộng: \(\overline x = \frac{{2.6 + 7 + 3.8 + 2.9 + 10}}{9} = \frac{{71}}{9}\)
+ Phương sai: \({S^2} = \frac{1}{9}({2.6^2} + {7^2} + {3.8^2} + {2.9^2} + {10^2}) - {\left( {\frac{{71}}{9}} \right)^2} = \frac{{134}}{{81}}\)
+ Độ lệch chuẩn: \(S = \sqrt {{S^2}} = \sqrt {\frac{{134}}{{81}}} = \frac{{\sqrt {134} }}{9}\)
Ta có: \(\frac{2}{3} < \frac{{134}}{{81}}\) nên kết quả thi của bạn Dũng ổn định hơn
