
Tính các tổng sau (Không sử dụng máy tính cầm tay):
a) \(T = C_4^0 + \frac{1}{2}C_4^1 + \frac{1}{3}C_4^2 + \frac{1}{4}C_4^3 + \frac{1}{5}C_4^4\)
b) \(S = C_6^1 + 2C_6^2 + 3C_6^3 + 4C_6^4 + 5C_5^6 + 6C_6^6\)

Bước 1: Ở ý a) áp dụng kết quả \(\frac{1}{{k + 1}}C_n^k = \frac{1}{{n + 1}}C_{n + 1}^{k + 1}\) với \(0 \le k \le n\) (chứng minh ở Bài 27a trang 14 SBT Toán 10 tập 2) và khai triển (a + b)5 với a = 1 và b = 1
Bước 2: Ở ý b) áp dụng kết quả \(kC_n^k = nC_{n - 1}^{k - 1}\) với \(1 \le k \le n\) (chứng minh ở Bài 27a trang 14 SBT Toán 10 tập 2) và khai triển (a + b)5 với a = 1 và b = 1

a) Áp dụng kết quả \(\frac{1}{{k + 1}}C_n^k = \frac{1}{{n + 1}}C_{n + 1}^{k + 1}\) với \(0 \le k \le n\) (chứng minh ở Bài 27a trang 14 SBT Toán 10 tập 2), ta được:

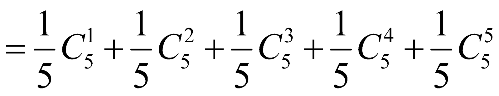
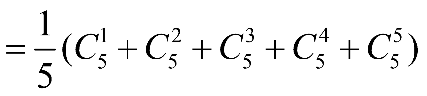
Advertisements (Quảng cáo)
Xét \({(a + b)^5} = C_5^0{a^5} + C_5^1{a^4}b + C_5^2{a^3}{b^2} + C_5^3{a^2}{b^3} + C_5^4a{b^4} + C_5^5{b^5}\)
Thay a = 1, b = 1 vào khai triển trên ta có: \({(1 + 1)^5} = C_5^0 + C_5^1 + C_5^2 + C_5^3 + C_5^4 + C_5^5\)
\( \Rightarrow C_5^0 + C_5^1 + C_5^2 + C_5^3 + C_5^4 + C_5^5 = {2^5} = 32\) \( \Rightarrow C_5^1 + C_5^2 + C_5^3 + C_5^4 + C_5^5 = 32 - C_5^0\)
Khi đó: \(T = \frac{1}{5}(C_5^1 + C_5^2 + C_5^3 + C_5^4 + C_5^5) = \frac{1}{5}(32 - C_5^0) = \frac{1}{5}(32 - 1)\)\( = \frac{{31}}{5}\)
Vậy \(T = \frac{{31}}{5}\)
b) Áp dụng kết quả \(kC_n^k = nC_{n - 1}^{k - 1}\) với \(1 \le k \le n\) (chứng minh ở Bài 27b trang 14 SBT Toán tập 2), ta được:
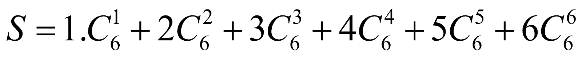

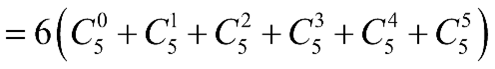
Theo a) ta có: \(C_5^0 + C_5^1 + C_5^2 + C_5^3 + C_5^4 + C_5^5 = {2^5} = 32\)
Khi đó: \(S = 6.(C_5^0 + C_5^1 + C_5^2 + C_5^3 + C_5^4 + C_5^5) = 6.32 = 192\)
Vậy S = 192
