
Gương phản chiếu của một đèn pha có mặt cắt là một parabol (P) với tim bóng đèn đặt ở tiêu điểm F. Chiều rộng giữa hai mép gương là 50 cm, chiều sâu của gương là 40 cm. Viết phương trình chính tắc của (P)

Parabol \(\left( P \right)\) có dạng \({y^2} = 2px\) với \(p > 0\) có tiêu điểm \(F\left( {\frac{p}{2};0} \right)\), phương trình đường chuẩn \(\Delta 😡 = - \frac{p}{2}\)

Gọi phương trình \(\left( P \right)\) có dạng \({y^2} = 2px\)
Advertisements (Quảng cáo)
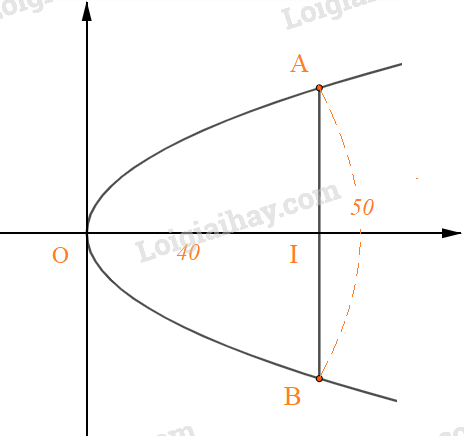
Khi đó gương là phần mặt phẳng tạo bởi đường cong AOB.
Ta có: Chiều rộng giữa hai mép gương là 50 cm, suy ra AB = 50cm.
Chiều sâu của gương là 40 cm suy ra OI = 40 cm.
Do đó AI = 50: 2= 25 và A(40; 25) thuộc vào parabol (P)
Thay điểm \(A\left( {40;25} \right)\) vào phương trình ta có \(p = \frac{{{y^2}}}{{2x}} = \frac{{{{25}^2}}}{{2.40}} \approx 7,8\)
\( \Rightarrow \left( P \right):{y^2} = 15,6x\)
