
Xác định giá trị của các hệ số a, b, c và xét dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\) trong mỗi trường hợp sau:
a) Đồ thị của hàm số \(y = f\left( x \right)\) đi qua ba điểm có tọa độ là \(\left( { - 1; - 4} \right),\left( {0;3} \right)\) và \(\left( {1; - 14} \right)\)
b) Đồ thị của hàm số \(y = f\left( x \right)\) đi qua ba điểm có tọa độ là \(\left( {0; - 2} \right),\left( {2;6} \right)\) và \(\left( {3;13} \right)\)
c) \(f\left( { - 5} \right) = 33,f\left( 0 \right) = 3\) và \(f\left( 2 \right) = 19\)

a) Giả sử tam thức bậc hai có công thức tổng quát là \(f\left( x \right) = a{x^2} + bx + c\)
Vì đồ thị của hàm số \(y = f\left( x \right)\) đi qua ba điểm có tọa độ là \(\left( { - 1; - 4} \right),\left( {0;3} \right)\) và \(\left( {1; - 14} \right)\) nên thay tọa độ của ba điểm vào phương trình tổng quát ta có:
\(\left\{ \begin{array}{l} - 4 = a{\left( { - 1} \right)^2} + b\left( { - 1} \right) + c\\3 = a{.0^2} + b.0 + c\\ - 14 = a{\left( 1 \right)^2} + b\left( 1 \right) + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a - b + c = - 4\\c = 3\\a + b + c = - 14\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 12\\b = - 5\\c = 3\end{array} \right.\)
Từ a, b, c đã xác định được ta có \(\Delta = 169 > 0\), tam thức có hai nghiệm phân biệt \(x = - \frac{3}{4}\) và \(x = \frac{1}{3}\), trong đó \(a = - 12 < 0\)
Ta có bảng biến thiên sau đây
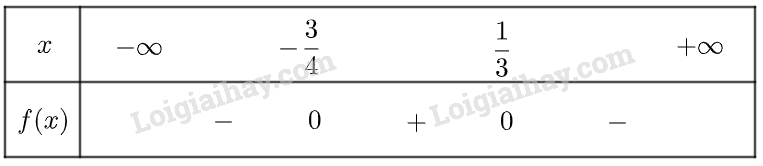
Vậy tam thức đã cho có dạng là \(f\left( x \right) = - 12{x^2} - 5x + 3\) dương trên khoảng \(\left( { - \frac{3}{4};\frac{1}{3}} \right)\), âm trên khoảng \(\left( { - \infty ; - \frac{3}{4}} \right)\) và \(\left( {\frac{1}{3}; + \infty } \right)\)
Advertisements (Quảng cáo)
b) Giả sử tam thức bậc hai có công thức tổng quát là \(f\left( x \right) = a{x^2} + bx + c\)
Vì đồ thị của hàm số \(y = f\left( x \right)\) đi qua ba điểm có tọa độ là \(\left( {0; - 2} \right),\left( {2;6} \right)\) và \(\left( {3;13} \right)\)
nên thay tọa độ của ba điểm vào phương trình tổng quát ta có:
\(\left\{ \begin{array}{l} - 2 = a{.0^2} + b.0 + c\\6 = a{.2^2} + b.2 + c\\13 = a{.3^2} + b.3 + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = - 2\\4a + 2b + c = 6\\9a + 3b + c = 13\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\\c = - 2\end{array} \right.\)
Từ a, b, c đã xác định được ta có \(\Delta = 12 > 0\), tam thức có hai nghiệm phân biệt \(x = - 1 - \sqrt 3 \) và \(x = - 1 + \sqrt 3 \), trong đó \(a = 1 > 0\)
Ta có bảng biến thiên sau đây

Vậy tam thức đã cho có dạng là \(f\left( x \right) = {x^2} + 2x - 2\) âm trên khoảng \(\left( { - 1 - \sqrt 3 ; - 1 + \sqrt 3 } \right)\), dương trên khoảng \(\left( { - \infty ; - 1 - \sqrt 3 } \right)\) và \(\left( { - 1 + \sqrt 3 ; + \infty } \right)\)
c) Giả sử tam thức bậc hai có công thức tổng quát là \(f\left( x \right) = a{x^2} + bx + c\)
Vì \(f\left( { - 5} \right) = 33\) nên \(a.{( - 5)^2} + b.( - 5) + c = 33\)
Vì \(f\left( 0 \right) = 3\) nên \(a{.0^2} + b.0 + c = 3\)
Vì \(f\left( 2 \right) = 19\) nên \(a{.2^2} + b.2 + c = 19\)
Từ đó ta có hệ
\(\left\{ \begin{array}{l}a.{( - 5)^2} + b.( - 5) + c = 33\\a{.0^2} + b.0 + c = 3\\a{.2^2} + b.2 + c = 19\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}25a - 5b + c = 33\\c = 3\\4a + 2b + c = 19\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}25a - 5b = 30\\4a + 2b = 16\\c = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 4\\c = 3\end{array} \right.\)
Vậy \(f(x) = 2{x^2} + 4x + 3\), có \(\Delta ‘ = {2^2} - 2.3 = - 2 < 0\) và \(a = 2 > 0\)nên \(f(x) > 0\) với mọi \(x \in \mathbb{R}\).
