Advertisements (Quảng cáo)
Cho tam giác ABC có trọng tâm G. Chứng minh các tam giác GBC, GAB, GAC có diện tích bằng nhau
Gọi AH, BK, CI là đường cao của tam giác ABC kẻ từ đỉnh A, B, C
GH’, GK’, GI’ là đường cao của tam giác GBC, GAC, GAB kẻ từ G xuống BC, AC, AB
Advertisements (Quảng cáo)
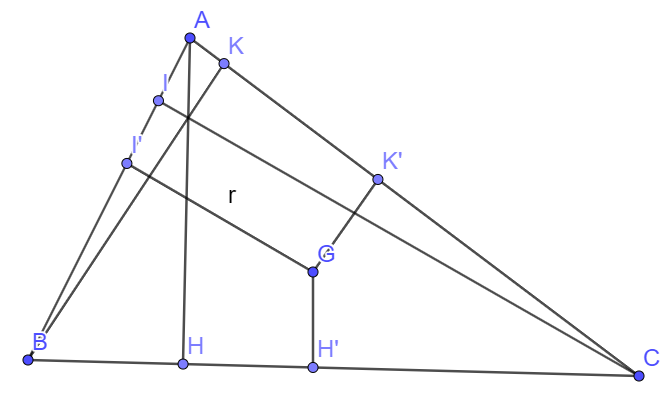
Ta có:
\({S_{GBC}} = \frac{1}{2}BC.GH’;{S_{GAC}} = \frac{1}{2}AC.GK’;{S_{GBA}} = \frac{1}{2}BA.GI’\)
Mà G là trọng tâm của tam giác ABC nên \(GH’ = \frac{1}{3}AH;GK’ = \frac{1}{3}BK;GI’ = \frac{1}{3}CI\)
Suy ra \({S_{GBC}} = \frac{1}{6}BC.AH;{S_{GAC}} = \frac{1}{6}AC.BK;{S_{GBA}} = \frac{1}{6}BA.CI\) (1)
Mặt khác ta có \({S_{ABC}} = \frac{1}{2}BC.AH = \frac{1}{2}AB.CI = \frac{1}{2}AC.BK\) (2)
Từ (1) và (2) ta có \({S_{GBC}} = {S_{GAB}} = {S_{GAC}} = \frac{1}{3}{S_{ABC}}\) (đpcm)