
Một xưởng sản xuất có 12 tấn nguyên liệu A và 8 tấn nguyên liệu B để sản xuất hai loại sản phẩm X, Y. Để sản xuất một tấn sản phẩm X cần dùng 6 tấn nguyên liệu A và 2 tấn nguyên liệu B, khi bán lãi được 10 triệu. Để sản xuất một tấn sản phẩm Y cần dùng 2 tấn nguyên liệu A và 2 tấn nguyên liệu B, khi bán được lãi 8 triệu đồng. Hãy lập ké hoạch sản xuất cho xưởng nói trên sao cho có tổng tiền lãi cao nhất

Gọi x, y lần lượt là số lượng sản phẩm X và Y (đơn vị: tấn) ta có hệ bất phương trình miêu tả diều kiện ràng buộc đối với x, y như sau:
\(\left\{ \begin{array}{l}6x + 2y \le 12\\2x + 2y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\)
Miền nghiệm của hệ bất phương trình là miền nghiệm tam giác ABCD, trong đó \(A(0;4),B\left( {1;3} \right),C(2;0),D(0;0)\)
Advertisements (Quảng cáo)
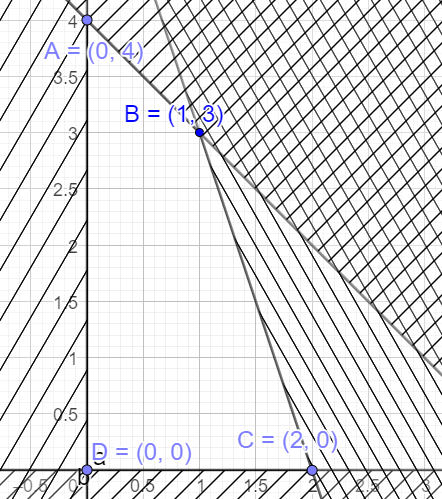
Gọi F là tổng tiền lãi thu được (đơn vị: triệu đồng) ta có: \(F = 10x + 8y\)
Tại \(A(0;4)\): \(F = 10.0 + 8.4 = 32\)
Tại \(B(1;3)\): \(F = 10.1 + 8.3 = 34\)
Tại \(C(2;0)\): \(F = 10.2 + 8.0 = 20\)
Tại \(D(0;0)\): \(F = 10.0 + 8.0 = 0\)
Ta thấy F đạt GTLN bằng 34 tại \(B(1;3)\)
Vậy xưởng nên lập kế hoạch sản xuất 1 sản phẩm X và 3 sản phẩm Y để thu về lãi cao nhất
