
Một phân xưởng có hai loại máy chuyên dụng \({M_1}\) và \({M_2}\) để sản xuất hai loại sản phẩm A và B theo đơn đặt hàng. Nếu sản xuất được một tấn sản phẩm loại A thì phân xưởng nhận được số tiền lãi là 2 triệu đồng. Nếu sản xuất được một tấn sản phẩm loại B thì phân xưởng nhận được số tiền lãi là 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A, người ta phải dùng máy \({M_1}\) trong 3 giờ và máy \({M_2}\) trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B, người ta phải dùng máy \({M_1}\) trong 1 giờ và máy \({M_2}\) trong 1 giờ. Một máy không thể dùng sản xuất đồng thời hai loại sản phẩm. Máy \({M_1}\) làm việc không quá 6 giờ một ngày và máy \({M_2}\) làm việc không quá 4 giờ một ngày. Hỏi số tiền lãi lớn nhất mà phân xưởng này có thể thu được trong một ngày là bao nhiêu?

- Viết hệ bất phương trình của bài toán nói trên
- Xác định miền nghiệm của hệ bất phương trình
- Viết biểu thức biểu thị số tiền lại phân xưởng thu được đạt giá trị lớn nhất

- Gọi \(x\) và \(y\) là số tấn sản phẩm loại A và loại B mà phân xưởng sản xuất được.
Điều kiện: \(x \ge 0;\,\,y \ge 0.\)
Thời gian máy \({M_1}\) làm việc không quá 6 giờ một ngày là: \(3x + y \le 6.\)
Thời gian máy \({M_2}\) làm việc không quá 4 giờ một ngày là: \(x + y \le 4.\)
Advertisements (Quảng cáo)
Ta có hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 6}\\{x + y \le 4}\end{array}.} \right.\)
Số tiền lãi phân xưởng này thu được trong một ngày là: \(F\left( {x;y} \right) = 2x + 1,6y \to \max \)
- Xác định miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 6}\\{x + y \le 4}\end{array}.} \right.\)
Miền nghiệm của bất phương trình \(d:x \ge 0\) là nửa mặt phẳng bờ \(d\) chứa điểm \(\left( {1;0} \right).\)
Miền nghiệm của bất phương trình \({d_1}:y \ge 0\) là nửa mặt phẳng bờ \({d_1}\) chứa điểm \(\left( {0;1} \right).\)
Miền nghiệm của bất phương trình \(3x + y \le 6\) là nửa mặt phẳng bờ \({d_2}:3x + y = 6\) chứa gốc tọa độ \(O\left( {0;0} \right).\)
Miền nghiệm của bất phương trình \(x + y \le 4\) là nửa mặt phẳng bờ \({d_3}:x + y = 4\) chứa gốc tọa độ \(O\left( {0;0} \right).\)
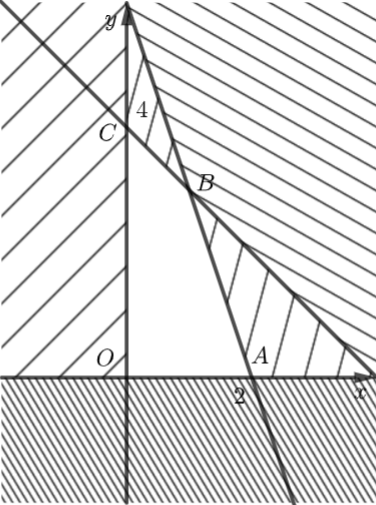
Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 6}\\{x + y \le 4}\end{array}} \right.\) là tứ giác \(OABC\) với \(A\left( {2;0} \right),\) \(B\left( {1;3} \right),\,\,C\left( {0;4} \right).\)
- Ta có: \(F\left( {2;0} \right) = 2.2 + 1,6.0 = 4;\,\,F\left( {0;0} \right) = 2.0 + 1,6.0 = 0;\)
\(F\left( {1;3} \right) = 2.1 + 1,6.3 = 6,8;\) \(F\left( {0;4} \right) = 2.0 + 1,6.4 = 6,4.\)
Vậy số tiền lãi lớn nhất phân xưởng này thu được trong một ngày là: 6,8 triệu đồng.
