
Cho tam giác \(OAB\) vuông cân, với \(OA = OB = a.\) Hãy xác định độ dài của các vectơ sau \(\overrightarrow {OA} + \overrightarrow {OB} ,\,\,\overrightarrow {OA} - \overrightarrow {OB} ,\,\,\overrightarrow {OA} + 2\overrightarrow {OB} ,\,\,2\overrightarrow {OA} - 3\overrightarrow {OB} .\)

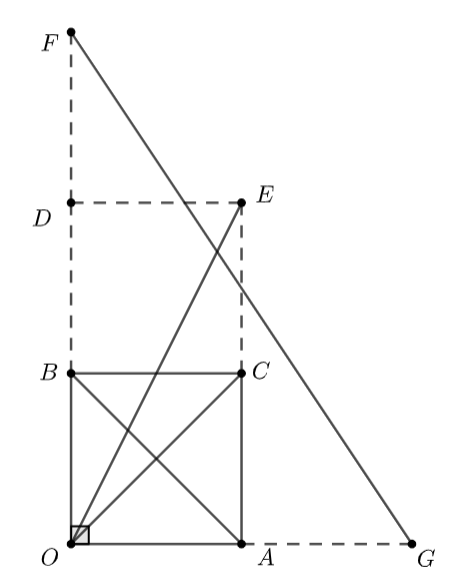
- Gọi \(D\) là điểm đối xứng với \(O\) qua \(B,\) \(F\) là điểm đối xứng với \(B\) qua \(D\) và \(G\) là điểm đối xứng với \(O\) qua \(A.\)
- Vẽ hình vuông \(OACB\) và hình chữ nhật \(OAED\)

+) Theo quy tắc hình bình hành, \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \) với C là đỉnh thứ tư của hình bình hành \(OACB\)
Ta có: tứ giác \(OACB\) là hình bình hành
mặt khác \(\Delta OAB\) vuông cân tại \(A\)
nên tứ giác \(OACB\) là hình bình hành
\( \Rightarrow \) \(\left| {\overrightarrow {OC} } \right| = OC = \sqrt {O{A^2} + O{B^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
+) Ta có: \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \)
Xét \(\Delta OAB\) vuông cân tại \(A\) có:
Advertisements (Quảng cáo)
\( \Rightarrow \) \(\left| {\overrightarrow {AB} } \right| = AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
+) Gọi điểm \(D\) là điểm đối xứng với \(O\) qua \(B\)
\( \Rightarrow \) \(2\overrightarrow {OB} = \overrightarrow {OD} \) và \(OD = 2a.\)
Theo quy tắc hình bình hành, ta có: \(\overrightarrow {OA} + 2\overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {OD} = \overrightarrow {OE} \) với \(E\) là điểm thứ tư của hình bình hành \(OAED\)
Ta có: tứ giác \(OAED\) là hình bình hành
Mặt khác \(\widehat {DOA} = {90^ \circ }\)
Nên tứ giác \(OAED\) là hình chữ nhật
Xét hình chữ nhật \(OAED\) có:
\( \Rightarrow \) \(\left| {\overrightarrow {OE} } \right| = OE = \sqrt {O{A^2} + O{D^2}} = \sqrt {{a^2} + {{\left( {2a} \right)}^2}} = a\sqrt 5 \)
+) Lấy điểm \(F\) đối xứng với \(B\) qua \(D\) và \(G\) đối xứng với \(O\) qua \(A\)
\( \Rightarrow \) \(2\overrightarrow {OA} = \overrightarrow {OG} ,\) \(3\overrightarrow {OB} = \overrightarrow {OF} ,\) \(OG = 2a,\)\(OF = 3a\)
Ta có: \(2\overrightarrow {OA} - 3\overrightarrow {OB} = \overrightarrow {OG} - \overrightarrow {OF} = \overrightarrow {FG} \)
Xét \(\Delta OFG\) vuông tại \(O\) có:
\( \Rightarrow \) \(\left| {\overrightarrow {FG} } \right| = FG = \sqrt {O{F^2} + O{G^2}} = \sqrt {{{\left( {3a} \right)}^2} + {{\left( {2a} \right)}^2}} = a\sqrt {13} \)
