
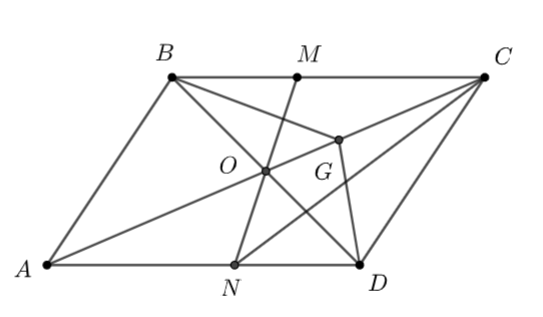
Cho hình bình hành \(ABCD\) tâm \(O.\) \(M\) là một điểm tùy ý thuộc cạnh \(BC,\) khác \(B\) và \(C.\) \(MO\) cắt cạnh \(AD\) tại \(N.\)
a) Chứng minh rằng \(O\) là trung điểm của \(MN.\)
b) Gọi \(G\) là trọng tâm của tam giác \(BCD.\) Chứng minh rằng \(G\) cũng là trọng tâm tam giác \(MNC.\)

- Chứng minh \(\Delta BOM = \Delta DON\)
- Chứng minh \(\overrightarrow {BM} = \overrightarrow {ND} \)
- Chứng minh \(\overrightarrow {GM} + \overrightarrow {GN} + \overrightarrow {GC} = \overrightarrow 0 \)

a) Xét \(\Delta BOM\) và \(\Delta DON\) có:
\(\widehat {BMO} = \widehat {DNO}\) (2 góc so le trong)
\(OB = OD\)
\(\widehat {BOM} = \overrightarrow {DOC} \) (2 góc đối đỉnh)
Advertisements (Quảng cáo)
\( \Rightarrow \) \(\Delta BOM = \Delta DON\) (g.c.g)
\( \Rightarrow \) \(OM = ON\) (2 cạnh tương ứng)
\( \Rightarrow \) \(O\) là trung điểm của \(MN\)
b) Ta có: \(G\) là trọng tâm của \(\Delta BCD\)
nên \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)
Ta có: \(\Delta BOM = \Delta DON\)
\( \Rightarrow \) \(BM = DN\)
Mặt khác \(BM\)//\(DN\)
\( \Rightarrow \) \(\overrightarrow {BM} = \overrightarrow {ND} \)
Xét \(\Delta MNC\):
\(\overrightarrow {GM} + \overrightarrow {GN} + \overrightarrow {GC} = \left( {\overrightarrow {GB} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {GD} + \overrightarrow {DN} } \right) + \overrightarrow {GC} \)
\( = \left( {\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} } \right) + \left( {\overrightarrow {BM} + \overrightarrow {DN} } \right) = \overrightarrow 0 \)
\( \Rightarrow \) \(G\) là trọng tâm của \(\Delta MNC\)
