
Cho đồ thị của hai hàm số bậc hai như dưới đây
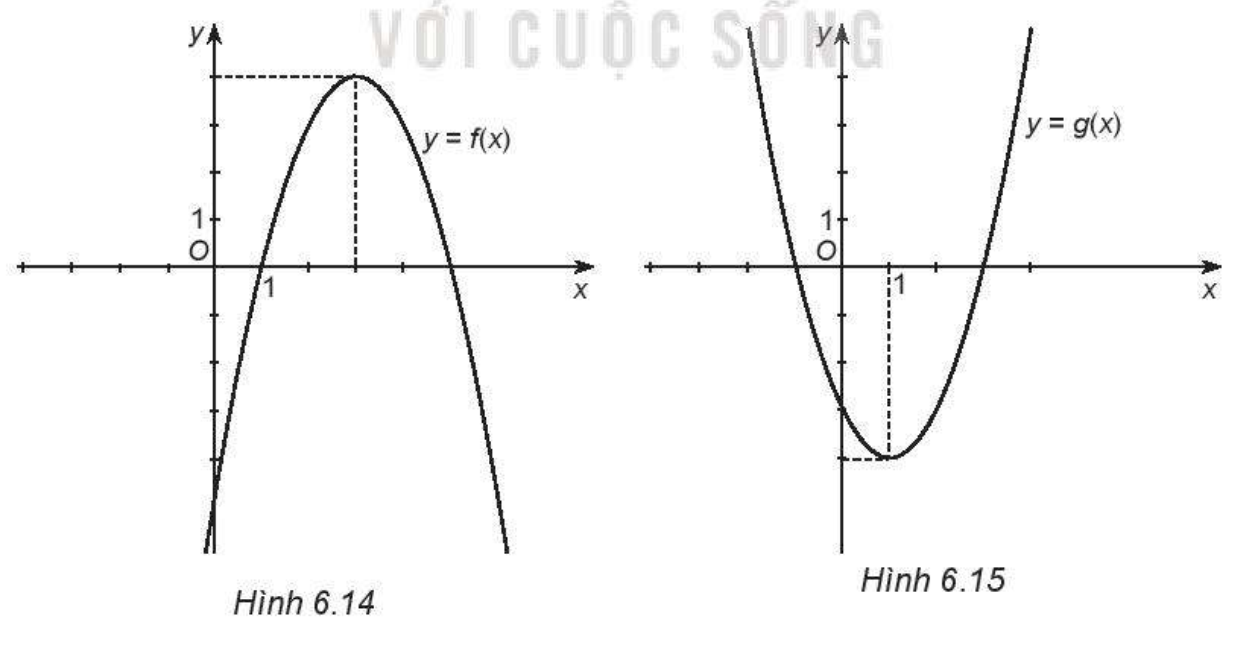
Với mỗi đồ thị, hãy:
a) Tìm tọa độ đỉnh của đồ thị
b) Tìm khoảng đồng biến và khoảng nghịch biến của hàm số
c) Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số
d) Tìm tập xác định và tập giá trị của hàm số

Dựa vào đồ thị, xác định các giá trị: tọa độ đỉnh, sự biến thiên, các khoảng giá trị của x và y để tìm các giá trị tương ứng theo yêu cầu đề bài

Advertisements (Quảng cáo)
a) Xét Hình 6.14
+) Đồ thị hàm số có đỉnh \({I_1}(3;4)\)
+) Hàm số đồng biến trên \(( - \infty ;3)\) và nghịch biến trên \((3; + \infty )\)
+) Hàm số có giá trị lớn nhất là 4, đạt được khi x = 3
+) Hàm số có tập xác định là \(\mathbb{R}\) và tập giá trị là \({\rm{( - }}\infty {\rm{;4]}}\)
b) Xét Hình 6.15
+) Đồ thị hàm số có đỉnh \({I_2}(1; - 4)\)
+) Hàm số nghịch biến trên \(( - \infty ;1)\) và đồng biến trên \((1; + \infty )\)
+) Hàm số có giá trị nhỏ nhất là -4, đạt được khi x = 1
+) Hàm số có tập xác định là \(\mathbb{R}\) và tập giá trị là \({\rm{[}} - 4; + \infty )\)
