I. Hàm số bậc hai
+ Định nghĩa:
Hàm số bậc hai là hàm số cho bằng công thức dạng \(y = a{x^2} + bx + c\) với \(a,b,c \in \mathbb{R};a \ne 0.\)
+ Tập xác định: \(\mathbb{R}\)
II. Đồ thị hàm số bậc hai
+) Đồ thị hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) \((a \ne 0)\) là một parabol (P):
- Đỉnh \(S\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\)
- Trục đối xứng: đường thẳng \(x = - \frac{b}{{2a}}\)
- Bề lõm: quay lên trên nếu \(a > 0\), quay xuống dưới nếu \(a < 0\)
- Cắt Oy tại điểm \((0;c)\)

* Chú ý: Nếu PT \(a{x^2} + bx + c = 0\) có hai nghiệm \({x_1},{x_2}\) thì đồ thị hàm số \(y = a{x^2} + bx + c\) cắt trục hoành tại 2 điểm có hoành độ lần lượt là 2 nghiệm này.
Advertisements (Quảng cáo)
+) Vẽ đồ thị
1) Xác định đỉnh \(S\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\)
2) Vẽ trục đối xứng d: \(x = - \frac{b}{{2a}}\)
3) Tìm tọa độ giao điểm của đồ thị với trục tung (A(0;c)), trục hoành (nếu có).
Xác định \(B\left( {\frac{{ - b}}{a};c} \right)\) (là điểm đối xứng với A qua d)
4) Vẽ parabol đỉnh S, trục đối xứng d, đi qua các điểm tìm được.
III. Ứng dụng
+) Bảng biến thiên
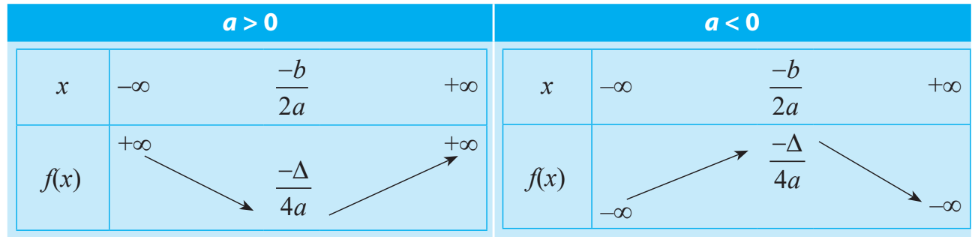
+) Ứng dụng của hàm số bậc hai
