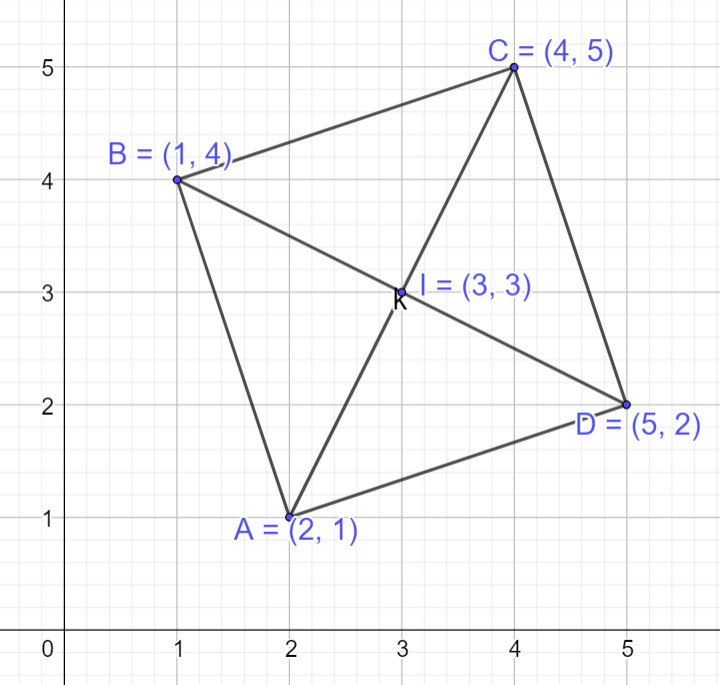
Trong mặt phẳng Oxy, cho bốn điểm \(A(2;1),B(1;4),C(4;5),D(5;2)\)
a) Chứng minh ABCD là một hình vuông
b) Tìm tọa độ tâm I của hình vuông ABCD

a) Bước 1: Tính AB, BC, CD, DA (Chứng minh AB=BC=CD=DA)
Bước 2: Chứng minh \(AB \bot BC\) thông qua tích vô hướng
b) Sử dụng tính chất trung điểm \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\) với M là trung điểm của AB
Advertisements (Quảng cáo)

a) Ta có: \(\overrightarrow {AB} = ( - 1;3),\overrightarrow {BC} = (3;1),\overrightarrow {CD} = (1; - 3),\overrightarrow {DA} = ( - 3; - 1)\)
Suy ra \(AB = BC = CD = DA = \sqrt {10} \)
Mặt khác \(\overrightarrow {AB} .\overrightarrow {BC} = ( - 1).3 + 3.1 = 0 \Rightarrow AB \bot BC\)
Vậy ABCD là hình vuông
b) Ta có ABCD là hình vuông, nên tâm I là trung điểm của đoạn thẳng AC
Vậy tọa độ điểm I là \(I(3;3)\)