
Cho AB và CD là hai dây cung vuông góc tại E của đường tròn (O) .Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ mặt phẳng để chứng minh EF vuông góc với DB

Bước 1: Xét với đường tròn bất kì, cho tọa độ các điểm A, B, C, D
Bước 2: Xác định tọa độ điểm E, F
Bước 3: Tính \(\overrightarrow {EF} .\overrightarrow {DB} \), suy ra vuông góc

Xét với đường tròn (O) có phương trình \((O):{\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 25\)
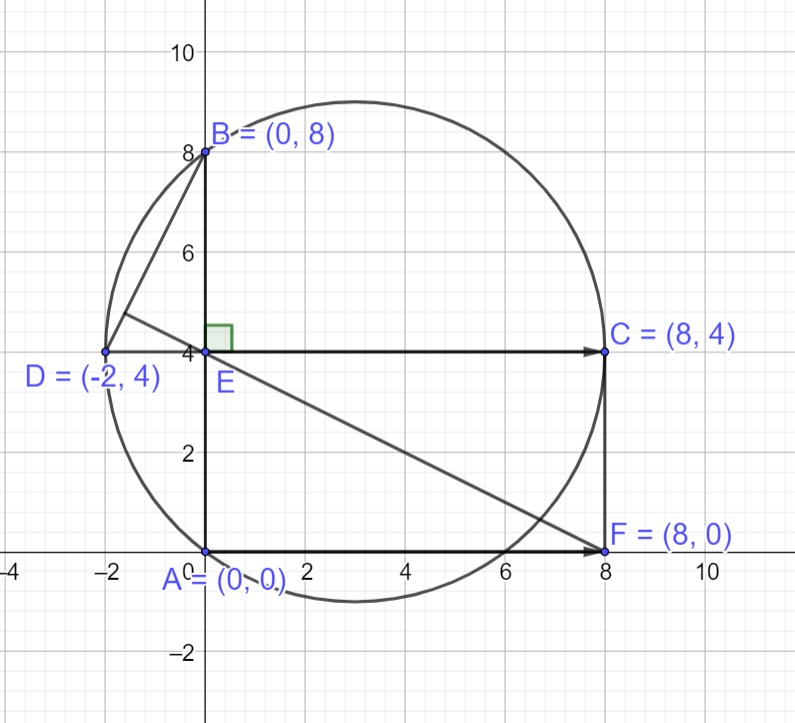
Cho các điểm \(A(0;0),B(0;8),C(8;4),D( - 2;4)\) nằm trên đường tròn (O) và thỏa mãn AB vuông góc với CD
Advertisements (Quảng cáo)
Phương trình đường thẳng đi qua hai điểm A, B có dạng \(x = 0\)
Phương trình đường thẳng đi qua hai điểm C, D có dạng \(y = 4\)
Ta có AB vuông góc với CD tại điểm E nên tọa độ điểm E là nghiệm của hệ sau:
\(\left\{ \begin{array}{l}x = 0\\y = 4\end{array} \right. \Leftrightarrow E(0;4)\)
Gọi tọa độ của điểm F là: \(F(x;y)\)
ACEF là hình chữ nhật nên \(\overrightarrow {AF} = \overrightarrow {EC} \), mặt khác ta có: \(\overrightarrow {AF} = (x;y),\overrightarrow {EC} = \left( {8;0} \right)\)
Suy ra tọa độ điểm F là: \(F\left( {8;0} \right)\)
\(\overrightarrow {EF} = \left( {8; - 4} \right),\overrightarrow {DB} = \left( {2;4} \right) \Rightarrow \overrightarrow {EF} .\overrightarrow {BD} = 8.2 + \left( { - 4} \right).4 = 0 \Rightarrow \overrightarrow {EF} \bot \overrightarrow {BD} \)
Vậy ta chứng minh được EF vuông góc với DB
