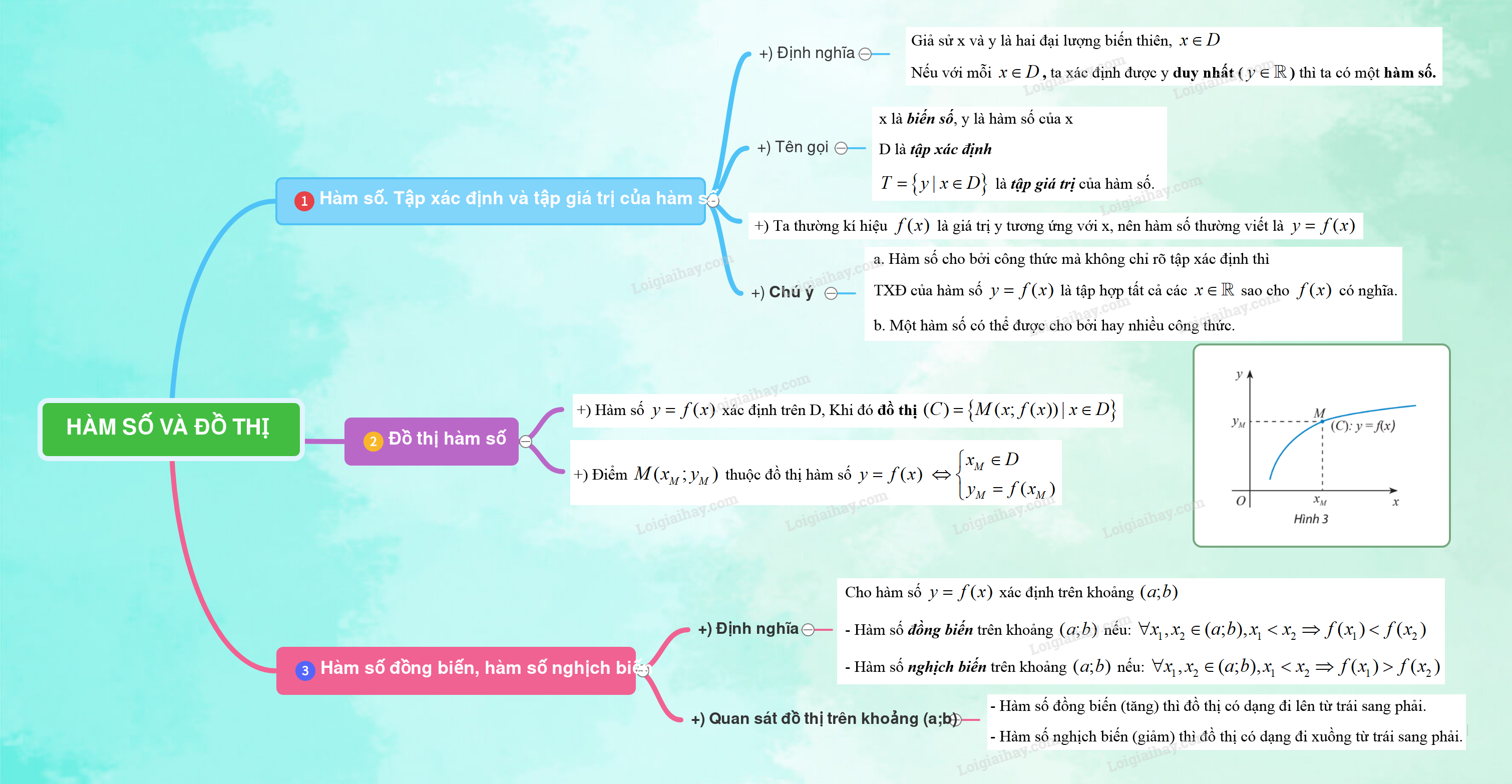
1. Hàm số. Tập xác định và tập giá trị của hàm số
+) Định nghĩa:
Giả sử x và y là hai đại lượng biến thiên, \(x \in D\)
Nếu với mỗi \(x \in D\), ta xác định được y duy nhất (\(y \in \mathbb{R}\)) thì ta có một hàm số.
+) Tên gọi:
x là biến số, y là hàm số của x
D là tập xác định
\(T = \left\{ {y|x \in D} \right\}\) là tập giá trị của hàm số.
+) Ta thường kí hiệu \(f(x)\) là giá trị y tương ứng với x, nên hàm số thường viết là \(y = f(x)\)
* Chú ý
a. Hàm số cho bởi công thức mà không chỉ rõ tập xác định thì
TXĐ của hàm số \(y = f(x)\) là tập hợp tất cả các \(x \in \mathbb{R}\) sao cho \(f(x)\) có nghĩa.
b. Một hàm số có thể được cho bởi hay nhiều công thức.
Advertisements (Quảng cáo)
2. Đồ thị hàm số
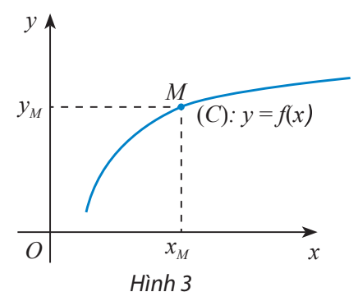
+) Hàm số \(y = f(x)\) xác định trên D, Khi đó đồ thị \((C) = \left\{ {M(x;f(x))|x \in D} \right\}\)
+) Điểm \(M({x_M};{y_M})\) thuộc đồ thị hàm số \(y = f(x)\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_M} \in D\\{y_M} = f({x_M})\end{array} \right.\)
3. Hàm số đồng biến, hàm số nghịch biến
+) Định nghĩa: Cho hàm số \(y = f(x)\) xác định trên khoảng \((a;b)\)
- Hàm số đồng biến trên khoảng \((a;b)\) nếu: \(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\)
- Hàm số nghịch biến trên khoảng \((a;b)\) nếu: \(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\)
+) Quan sát đồ thị: trên khoảng \((a;b)\)
- Hàm số đồng biến (tăng) thì đồ thị có dạng đi lên từ trái sang phải.
- Hàm số nghịch biến (giảm) thì đồ thị có dạng đi xuồng từ trái sang phải.