HĐ Khám phá 2
Trong mặt phẳng Oxy, cho hai vectơ \(\overrightarrow a = \left( {{a_1},{a_2}} \right),\overrightarrow b = \left( {{b_1},{b_2}} \right)\) và số thực k. Ta đã biết có thể biểu diễn từng vectơ \(\overrightarrow a ,\overrightarrow b \) theo hai vectơ , \(\overrightarrow j \) như sau
a) Biểu diễn từng vectơ \(\overrightarrow a + \overrightarrow b ,\overrightarrow a - \overrightarrow b ,k\overrightarrow a \) theo hai vectơ , \(\overrightarrow j \)
b) Tìm \(\overrightarrow a .\overrightarrow b \) theo tọa độ của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \)

a) Ta có
\(\begin{array}{*{20}{l}}
{\vec a + \vec b = \left( {{a_1} + {a_2}\vec j} \right) + \left( {{b_1} + {b_2}\vec j} \right) = \left( {{a_1} + {b_1}} \right) + \left( {{a_2} + {b_2}} \right)}\\
{\vec a - \vec b = \left( {{a_1} + {a_2}\vec j} \right) - \left( {{b_1} + {b_2}\vec j} \right) = \left( {{a_1} - {b_1}} \right) + \left( {{a_2} - {b_2}} \right)}\\
{k\vec a = k\left( {{a_1} + {a_2}\vec j} \right) = k{a_1} + k{a_2}\vec j}
\end{array}\)
b) Ta có
\(\begin{array}{l}
\vec a.\vec b = \left( {{a_1}\overrightarrow i + {a_2}\vec j} \right).\left( {{b_1}\overrightarrow i + {b_2}\vec j} \right)\\
= {a_1}{b_1}{\overrightarrow i ^2} + {a_1}{b_2}\overrightarrow i .\vec j + {a_2}{b_1}\overrightarrow i \vec j + {a_2}{b_2}{{\vec j}^2}\\
= {a_1}{b_1} + {a_2}{b_2}
\end{array}\)
Vì \({\overrightarrow i ^2} = {\left| {\overrightarrow i } \right|^2} = 1,{\overrightarrow j ^2} = {\left| {\overrightarrow j } \right|^2} = 1,\overrightarrow i \overrightarrow j = 0\)
Thực hành 2
Cho hai vectơ \(\overrightarrow m = \left( { - 6;1} \right),\overrightarrow n = \left( {0;2} \right)\)
a) Tìm tọa độ các vectơ \(\overrightarrow m + \overrightarrow n ,\overrightarrow m - \overrightarrow n ,10\overrightarrow m , - 4\overrightarrow n \)
b) Tính các tích vô hướng \(\overrightarrow m .\overrightarrow n ,\left( {10\overrightarrow m } \right).\left( { - 4\overrightarrow n } \right)\)

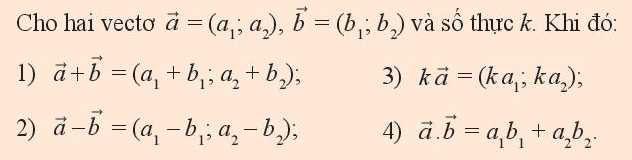
Advertisements (Quảng cáo)

a) Ta có
\(\begin{array}{l}\overrightarrow m + \overrightarrow n = \left( {\left( { - 6 + 0} \right);1 + 2} \right) = ( - 6;3)\\\overrightarrow m - \overrightarrow n = \left( {\left( { - 6 - 0} \right);\left( {1 - 2} \right)} \right) = \left( { - 6; - 1} \right)\\10\overrightarrow m = (10.( - 6);10.1) = ( - 60;10)\\ - 4\overrightarrow n = (( - 4).0;( - 4).2) = (0; - 8)\end{array}\)
b) Ta có
\(\overrightarrow m .\overrightarrow n = ( - 6).0 + 1.2 = 0 + 2 = 2\)
Ta có \(10\overrightarrow m = ( - 60;10)\) và \( - 4\overrightarrow n = (0; - 8)\) nên \(\left( {10\overrightarrow m } \right).\left( { - 4\overrightarrow n } \right) = ( - 60).0 + 10.( - 8) = 0 - 80 = - 80\)
Vận dụng 2
Một thiết bị thăm dò đáy biển đang lặn với vận tốc \(\overrightarrow v = \left( {10; - 8} \right)\) (hình 8). Cho biết vận tốc của dòng hải lưu vùng biển là \(\overrightarrow w = \left( {3,5;0} \right)\). Tìm tọa dộ của vectơ tổng hai vận tốc \(\overrightarrow v \) và \(\overrightarrow w \)
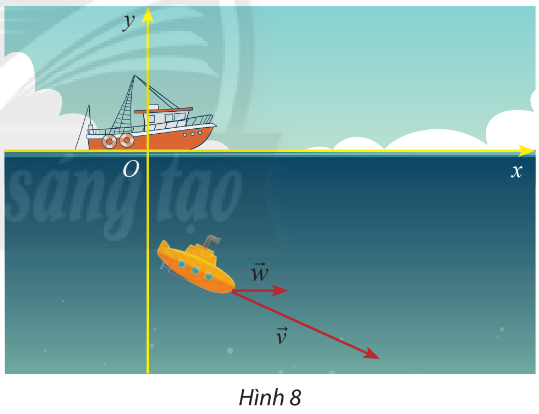

Với \(\overrightarrow v = \left( {{v_1};{v_2}} \right),\overrightarrow w = \left( {{w_1};{w_2}} \right)\) thì \(\overrightarrow v + \overrightarrow w \) là \(\left( {{v_1} + {w_1};{v_2} + {w_2}} \right)\)

\(\overrightarrow v + \overrightarrow w = (10 + 3,5;( - 8) + 0) = (13,5; - 8)\)
Vậy tọa độ của vectơ tổng hai vận tốc \(\overrightarrow v \) và \(\overrightarrow w \) là \((13,5; - 8)\)
