Bài 3.9 trang 43 Toán 10 tập 1: Trên nóc một tòa nhà có một cột ăng – ten cao 5m, Từ một vị trí quan sát A cao 7m so với mặt đất có thể nhìn...

Hướng dẫn giải bài 3.9 trang 43 SGK Toán lớp 10 tập 1 Kết nối tri thức. Bài 6: Hệ thức lượng trong tam giác

 

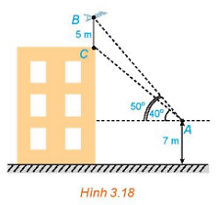
Trên nóc một tòa nhà có một cột ăng – ten cao 5m, Từ một vị trí quan sát A cao 7m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng – ten, với các góc tương ứng là 50⁰ và 40⁰ so với phương nằm ngang (H.3.18).

a) Tính các góc của tam giác ABC.

b) Tính chiều cao của tòa nhà.

Ta có hình vẽ sau:

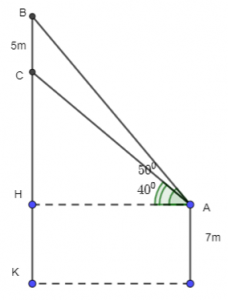
a) Ta có:

∠BAC = 50º – 40º = 10º

Xét ΔABH, vuông tại H, có:

∠CBA + ∠BAH = 90º (hai góc phụ nhau)

⇒ ∠CBA = 90º  – ∠BAH = 90⁰ – 50⁰ = 40⁰

Xét ΔABC, có:

∠ACB = 180º – ∠BAC – ∠CBA = 180⁰ – 10⁰ – 40⁰ = 130⁰.

b) Xét ΔABC, có:

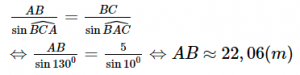
Xét ΔABH, có:

BH = sin∠BAC.AB ≈ sin50⁰.22,06 ≈ 16,9(m)

Do đó chiều cao của tòa nhà là: 16,9 + 7 = 23,9 (m).

Vậy chiều cao của tòa nhà là 23,9 m.