Hướng dẫn giải bài 4.17 trang 65 SGK Toán lớp 10 tập 1 Kết nối tri thức. Bài 10: Vectơ trong mặt phẳng tọa độ
Trong mặt phẳng tọa độ Oxy, cho các vectơ 
và các điểm M(-3;6), N(3;-3).
a) Tìm mối liên hệ giữa các vectơ →MN và 2→a - →b
b) Các điểm O, M, N có thẳng hàng hay không?
c) Tìm điểm P(x;y) để OMPN là hình bình hành.
a) Ta có →b = (4; -1) và →a = 3 . →i – 2. →j => →a (3; -2)
=> 2 →a – →b = ( 2.3 – 4 ; 2. (-2) – ( -1)) = (2; -3)
Lại có: M (-3; 6) , N (3; -3)
=> →MN = (3 – (-3); -3 – 6) = (6: -9)
Ta thấy: (6; -9) = 3. (2; -3) => →MN = 3 (2 →a – →b)
b)
Advertisements (Quảng cáo)
Ta có →OM = (-3; 6) (do M (-3; 6) và →ON = (3; -3) (do N (3; -3)
Hai vectơ này không cùng phương 
.
Do đó các điểm O, M, N không cùng nằm trên một đường thẳng.
Vậy chúng không thẳng hàng.
Ta có →b = (4; -1) và →a = 3 . →I – 2. →J => →a (3; -2)
=> 2 →a – →b = ( 2.3 – 4 ; 2. (-2) – ( -1)) = (2; -3)
Lại có: M (-3; 6) , N (3; -3)
=> →MN = (3 – (-3); -3 – 6) = (6: -9)
Ta thấy: (6; -9) = 3. (2; -3) => →MN = 3 (2 →a – →b)
c) Các điểm O, M, N không thẳng hàng nên OMNP là một hình hành khi và chỉ khi OM = → PN
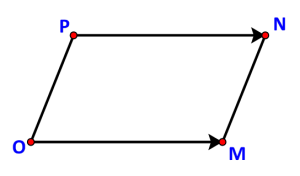
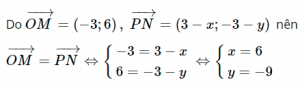
Vậy điểm cần tìm là P (6; -9)