Hướng dẫn giải bài 4.24 trang 70 SGK Toán lớp 10 tập 1 Kết nối tri thức. Bài 11: Tích vô hướng của hai vectơ
![]()
Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(-4;1), B(2;4), C(2;-2)
a) Giải tam giác ABC.
b) Tìm tọa độ trực tâm H của tam giác ABC.
![]()
a) Ta có:
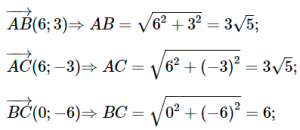
Áp dụng định lí cosin cho tam giác ABC, ta có:
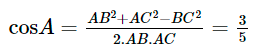
⇒ góc A ≈ 53,13º
Tam giác ABC có AB = AC nên tam giác ABC cân tại A
Advertisements (Quảng cáo)
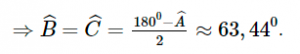
Vậy AB = AC = 3√5 , BC = 6
∠A = 53,13º , ∠B = ∠C = 63,44º
b) Gọi trực tâm H của tam giác ABC có tọa độ là H(x;y)
Khi đó, ta có:
→AH(x+4;y−1); →BC(0;−6); →BH(x−2;y−4); →AC(6;−3)
Vì AH ⊥ BC ⇒ →AH . →BC = 0 ⇔ (x + 4).0 + (y – 1).(–6) = 0 ⇔ y = 1
Vì BH ⊥ AC ⇒ →BH . →AC = 0 ⇔ (x – 2).6 + (y – 4).(–3) = 0
⇔ (x – 2).2 + (y – 4).(–1) = 0
⇔ 2x – y = 0
Mà y = 1 ⇒ 2x – 1 = 0 ⇔ x = 1/2
