Cho các phương trình:
\(x^2+ 3x - m + 1 = 0\) (1) và \(2x^2- x + 1 - 2p = 0\) (2)
a) Biện luận số nghiệm của mỗi phương trình bằng đồ thị.
b) Kiểm tra lại kết quả trên bằng phép tính.

a)
* Xét phương trình \({x^2} + {\rm{ }}3x{\rm{ }}-{\rm{ }}m{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}0\)
Ta có: (1) \( \Leftrightarrow {\rm{ }}{x^2} + {\rm{ }}3x{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}m{\rm{ }}\)
Gọi (d) là đường thẳng \(y = m\).
Đồ thị hàm số \(y = x^2+ 3x + 1\) là parabol (P) có đỉnh là điểm \((-1,5; -1,25)\) và hướng bề lõm lên trên.
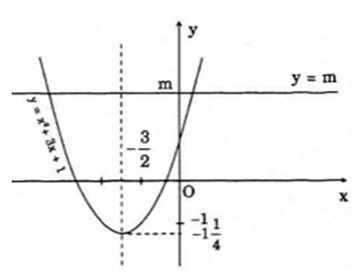
Do đó:
Advertisements (Quảng cáo)
+ Khi \(m < -1, 25\) thì (d) không cắt (P), phương trình vô nghiệm.
+ Khi \(m = -1,25\) thì (d) và (P) có một điểm chung, phương trình có một nghiệm.
+ Khi \(m > -1,25\) thì (d) cắt (P) tại hai điểm. Phương trình có hai nghiệm phân biệt.
* Xét phương trình \(2x^2- x + 1 – 2p = 0\) (2)
(2) \(⇔ 2x^2 – x + 1 = 2p\)
Gọi (d) là đường thẳng \(y = 2p\); (P) là parabol \(y = 2x^2– x + 1 \)
Parabol (P) có đỉnh tại điểm: \(({1 \over 4};\,{7 \over 8})\) và hướng bề lõm lên trên.
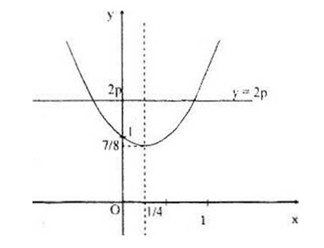
Do đó:
+ Nếu \(2p < {7 \over 8}\) , tức là \(p < {7 \over {16}}\) thì (d) không cắt (P), phương trình vô nghiệm.
+ Nếu \(2p = {7 \over 8}\) , tức là \(p = {7 \over {16}}\) thì (d) và (P) có một điểm chung, phương trình có một nghiệm.
+ Nếu \(2p > {7 \over 8}\) , tức là \(p > {7 \over {16}}\) thì (d) cắt (P) tại hai điểm chung, phương trình có hai nghiệm.
