Bài 6
a) Xét dấu biểu thức
\(f(x) = 2x(x+2) – (x+2)(x+1)\)
b) Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc các đồ thị của các hàm số sau
\(y = 2x(x+2) (C_1)\)
\(y = (x+2)(x+1) (C_2)\)
Tính tọa độ các giao điểm \(A\) và \(B\) của \((C_1)\) và \((C_2)\)
c) Tính các hệ số \(a, b, c\) để hàm số \(y = ax^2+ bx + c\) có giá trị lớn nhất bằng \(8\) và đồ thị của nó đi qua \(A\) và \(B\).
a) \(f(x) = (x+2)(x-1)\)
\(f(x) > 0\) với \(x < -2\) hoặc \(x > 1\)
\(f(x) ≤ 0\) với \(-2 ≤ x ≤ 1\)
b) \(y = 2x (x + 2) = 2(x+1)^2– 2\)
Advertisements (Quảng cáo)
Bảng biến thiên:
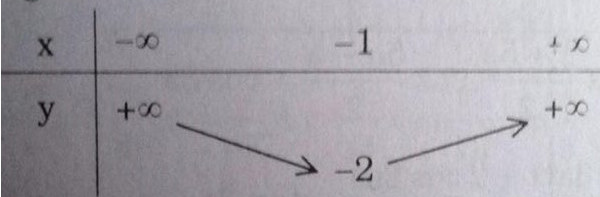
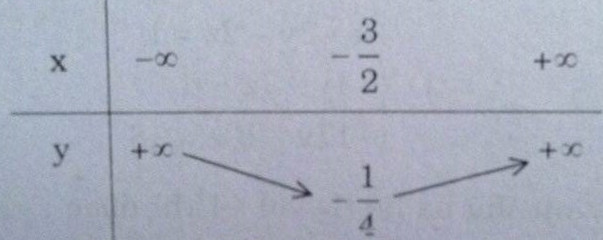
Hàm số : \(y{\rm{ }} = \left( {x + 2} \right)\left( {x + 1} \right) = {(x + {3 \over 2})^2} - {1 \over 4}\)
Bảng biến thiên
Đồ thị (C1) và (C2)
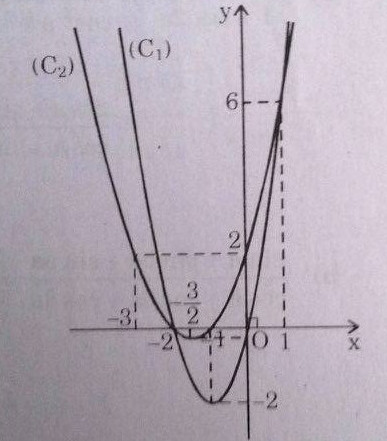
Hoành độ các giao điểm \(A\) và \(B\) của (C1) và (C2) là nghiệm của phương trình \(f(x) = 0 ⇔ x_1= -2, x_2= 1\)
\(⇔ A(-2; 0) , B(1; 6)\)
c) Giải hệ phương trình
\(\left\{ \matrix{
{{ac - {b^2}} \over {4a}} \hfill \cr
a{( - 2)^2} + b( - 2) + c = 0 \hfill \cr
a{(1)^2} + b(1) + c = 6 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = - 2,b = 0,c = 8 \hfill \cr
a = - {2 \over 9},b = {{16} \over 9},c = {{40} \over 9} \hfill \cr} \right.\)
