Một ô tô đang chuyển động với vận tốc không đổi 30m/s. Đến chân một con dốc, đột nhiên máy ngừng hoạt động và ô tô theo đà đi lên dốc. Nó luôn chịu một gia tốc ngược chiều vận tốc đầu bằng 2m/s2 trong suốt quá trình lên dốc và xuống dốc.
a) Viết phương trình chuyển động của ô tô, lấy gốc tọa độ x = 0 và gốc thời gian t = 0 lúc xe ở vị trí chân dốc.
b) Tính quãng đường xa nhất theo sườn dốc mà ô tô có thể lên được.
c) Tính thời gian đi hết quãng đường đó.
d) Tính vận tốc của ô tô sau 20s. Lúc đó ô tô chuyển động theo chiều nào?

a)
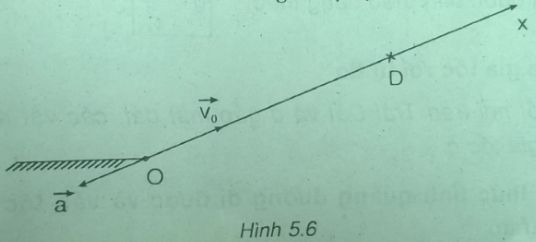
Chọn gốc tọa độ O tại chân dốc, chiều dương hướng lên. Gốc thời gian là lúc bắt đầu lên dốc thì các giá trị đại số:
Advertisements (Quảng cáo)
v0 = 30 (m/s); a = -2 (m/s2); x0 = 0 (\(\overrightarrow {{v_0}} \) cùng chiều dương nên v0 > 0; \(\overrightarrow a \) ngược chiều dương nên a < 0
Phương trình chuyển động của xe:
\(x = 30t - {t^2}\,\,\left( {s;\,m} \right)\)
b) a.v0 < 0 ⇔ xe chuyển động chậm dần đều, lên tới điểm D rồi đổi chiều, chuyển động nhanh dần đều xuống:
Tại D có \(v = 0 \Rightarrow \Delta x = {{ - v_0^2} \over {2{\rm{a}}}} = {{ - {{30}^2}} \over {2\left( { - 2} \right)}} = 225\left( m \right)\)
Quãng đường xa nhất OD = |∆x| = 225 (m)
c) \(v = {v_0} + at \Rightarrow t = {{v - {v_0}} \over a} = {{ - {v_0}} \over a} = {{ - 30} \over { - 2}} = 15\left( s \right)\)
d) Tại t = 20 (s) có: v = 30 – 2.20 = -10 (m/s)
v < 0 ⇔ lúc này xe đang xuống dốc.
