Để chứng minh \(AM\parallel \left( {A’NC} \right)\), ta cần chứng minh rằng \(AM\) song song với một đường thẳng nào đó trong mặt phẳng \(\left( {A’NC} \right)\). Lời Giải - Bài 60 trang 118 sách bài tập toán 11 - Cánh diều - Bài tập cuối chương IV. Cho hình lăng trụ tam giác \(ABC. A'B'C'\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(BC\), \(B'C'\)...

Cho hình lăng trụ tam giác \(ABC.A’B’C’\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(BC\), \(B’C’\). Chứng minh rằng \(AM\parallel \left( {A’NC} \right)\).

Để chứng minh \(AM\parallel \left( {A’NC} \right)\), ta cần chứng minh rằng \(AM\) song song với một đường thẳng nào đó trong mặt phẳng \(\left( {A’NC} \right)\).

Advertisements (Quảng cáo)
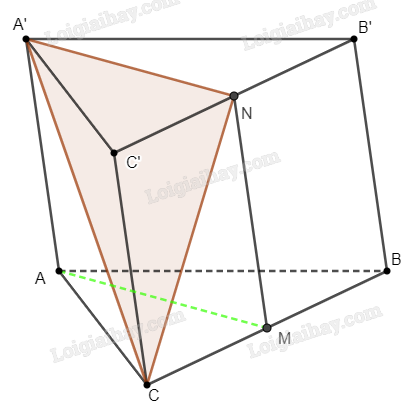
Do \(M\) là trung điểm của \(BC\), \(N\) là trung điểm của \(B’C’\) nên ta suy ra \(MN = BB’\) và \(MN\parallel BB’\). Suy ra \(MN\parallel AA’\) và \(MN = AA’\). Như vậy tứ giác \(AMNA’\) là hình bình hành, từ đó \(AM\parallel A’N\).
Mà \(A’N \subset \left( {A’NC} \right)\), ta suy ra \(AM\parallel \left( {A’NC} \right)\).
Bài toán được chứng minh.
