
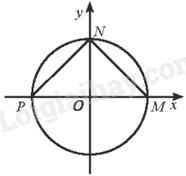
Cho ba điểm M, N, P lần lượt là các điểm biểu diễn trên đường tròn lượng giác của các góc lượng giác có số đo \(k2\pi ,\frac{\pi }{2} + k2\pi ,\pi + k2\pi \left( {k \in \mathbb{Z}} \right)\). Tam giác MNP là tam giác gì?

Sử dụng kiến thức về biểu diễn góc lượng giác trên đường tròn lượng giác.

Advertisements (Quảng cáo)
Vì điểm M biểu diễn trên đường lượng giác các góc lượng giác có số đo \(k2\pi \left( {k \in \mathbb{Z}} \right)\) nên \(M\left( {1;0} \right)\).
Vì điểm N biểu diễn trên đường lượng giác các góc lượng giác có số đo \(\frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\) nên \(N\left( {0;1} \right)\).
Vì điểm P biểu diễn trên đường lượng giác các góc lượng giác có số đo \(\pi + k2\pi \left( {k \in \mathbb{Z}} \right)\) nên \(P\left( { - 1;0} \right)\).
Do đó, \(PM = 2,NP = MN = \sqrt 2 \)
Vì \(M{N^2} + N{P^2} = P{M^2}\) nên tam giác MNP vuông N.
Lại có: \(NP = MN = \sqrt 2 \) nên tam giác MNP vuông cân tại N.
