
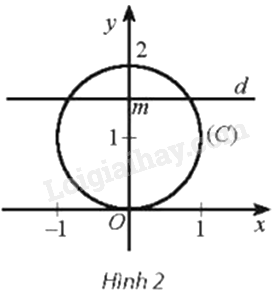
Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{x^2} + {\left( {y - 1} \right)^2} = 1\). Với mỗi số thực m, gọi Q(m) là số giao điểm của đường thẳng \(d:y = m\) với đường tròn (C). Viết công thức xác định hàm số \(y = Q\left( m \right)\). Hàm số này không liên tục tại các điểm nào?

Sử dụng kiến thức về định nghĩa hàm số liên tục tại một điểm để xét tính liên tục của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng K và \({x_0} \in K\). Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại điểm \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
Advertisements (Quảng cáo)

\(Q\left( m \right) = \left\{ \begin{array}{l}0\;khi\;m 2\\1\;khi\;m = 0\;hay\;m = 2\\2\;khi\;0
Vì \(\mathop {\lim }\limits_{m \to {0^ + }} Q\left( m \right) \ne \mathop {\lim }\limits_{m \to {0^ - }} Q\left( m \right)\) nên hàm số trên không liên tục tại điểm \(m = 0\).
Vì \(\mathop {\lim }\limits_{m \to {2^ + }} Q\left( m \right) \ne \mathop {\lim }\limits_{m \to {2^ - }} Q\left( m \right)\) nên hàm số trên không liên tục tại điểm \(m = 2\).
Vậy hàm số Q(m) không liên tục tại các điểm \(m = 0\), \(m = 2\).
