
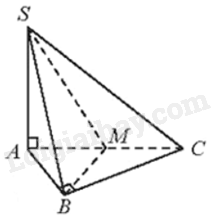
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và \(SA \bot \left( {ABC} \right)\).
a) Chứng minh rằng \(\left( {SBC} \right) \bot \left( {SAB} \right)\).
b) Gọi M là trung điểm của AC. Chứng minh rằng \(\left( {SBM} \right) \bot \left( {SAC} \right)\)

Sử dụng kiến thức về điều kiện để hai mặt phẳng vuông góc: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

Advertisements (Quảng cáo)
a) Vì tam giác vuông cân tại B nên \(AB \bot BC\)
Lại có: \(SA \bot \left( {ABC} \right),BC \subset \left( {ABC} \right) \Rightarrow SA \bot BC\)
Do đó, \(BC \bot \left( {SAB} \right)\), mà \(BC \subset \left( {SBC} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)\)
b) Vì tam giác vuông cân tại B nên BM là đường trung tuyến đồng thời là đường cao.
Do đó, \(BM \bot AC\)
Lại có: \(SA \bot \left( {ABC} \right),BM \subset \left( {ABC} \right) \Rightarrow SA \bot BM\)
Do đó, \(BM \bot \left( {SAC} \right)\), mà \(BM \subset \left( {SBM} \right) \Rightarrow \left( {SBM} \right) \bot \left( {SAC} \right)\)
