
Cho hàm số \(y = \tan x\) với \(x \in \left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right) \cup \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
a) Vẽ đồ thị của hàm số đã cho.
b) Tìm các giá trị của \(x \in \left[ { - \frac{{7\pi }}{4};\frac{\pi }{4}} \right]\) sao cho \(\sqrt 3 \tan \left( {x + \frac{\pi }{4}} \right) + 1 = 0\).
c) Tìm các giá trị của \(x \in \left[ { - \frac{{5\pi }}{6};\frac{\pi }{6}} \right]\) sao cho \(\tan \left( {2x + \frac{\pi }{6}} \right) \ge - \frac{{\sqrt 3 }}{3}\).

Sử dụng kiến thức về đồ thị hàm số \(y = \tan x\) để giải.

a) Ta có đồ thị của hàm số \(y = \tan x\) với \(x \in \left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right) \cup \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\):
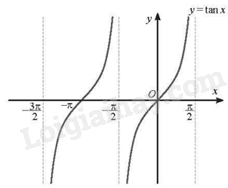
b) \(\sqrt 3 \tan \left( {x + \frac{\pi }{4}} \right) + 1 = 0\) khi \(\tan \left( {x + \frac{\pi }{4}} \right) = \frac{{ - \sqrt 3 }}{3}\)
Đặt \(x + \frac{\pi }{4} = t\). Vì \(\frac{{ - 7\pi }}{4} \le x \le \frac{\pi }{4} \Rightarrow \frac{{ - 3\pi }}{2} \le t \le \frac{\pi }{2}\)
Hàm số \(y = \tan t\) xác định khi \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\). Kết hợp với điều kiện \(\frac{{ - 3\pi }}{2} \le t \le \frac{\pi }{2}\) ta có \(t \in \left( {\frac{{ - 3\pi }}{2};\frac{{ - \pi }}{2}} \right) \cup \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\).
Advertisements (Quảng cáo)
Đồ thị hàm số \(y = \tan t\) với \(t \in \left( {\frac{{ - 3\pi }}{2};\frac{{ - \pi }}{2}} \right) \cup \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\) là:
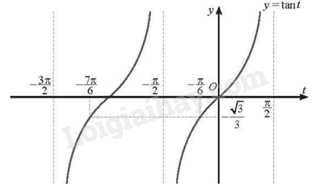
Từ đồ thị hàm số trên ta có:
\(\tan t = \frac{{ - \sqrt 3 }}{3}\) khi và chỉ khi \(t = \frac{{ - 7\pi }}{6}\) hoặc \(t = \frac{{ - \pi }}{6}\).
Suy ra: \(x + \frac{\pi }{4} = \frac{{ - 7\pi }}{6}\) hoặc \(x + \frac{\pi }{4} = \frac{{ - \pi }}{6}\). Do đó, \(x = \frac{{ - 17\pi }}{{12}}\) hoặc \(x = \frac{{ - 5\pi }}{{12}}\).
c) Đặt \(2x + \frac{\pi }{6} = t\). Vì \(\frac{{ - 5\pi }}{6} \le x \le \frac{\pi }{6} \Rightarrow \frac{{ - 3\pi }}{2} \le t \le \frac{\pi }{2}\)
Hàm số \(y = \tan t\) xác định khi \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\). Kết hợp với điều kiện \(\frac{{ - 3\pi }}{2} \le t \le \frac{\pi }{2}\) ta có \(t \in \left( {\frac{{ - 3\pi }}{2};\frac{{ - \pi }}{2}} \right) \cup \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\)
Đồ thị hàm số \(y = \tan t\) với \(t \in \left( {\frac{{ - 3\pi }}{2};\frac{{ - \pi }}{2}} \right) \cup \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\) là:
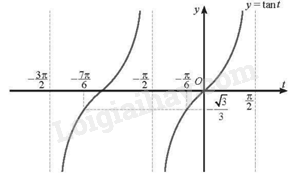
Từ đồ thị hàm số trên ta có:
\(\tan t \ge \frac{{ - \sqrt 3 }}{3}\) khi và chỉ khi \(\frac{{ - 7\pi }}{6} \le t
Suy ra, \(\frac{{ - 7\pi }}{6} \le 2x + \frac{\pi }{6}
Do đó, \(\frac{{ - 2\pi }}{3} \le x
