Trên đường tròn lượng giác, xác định điểm Q biểu diễn các góc lượng giác có số đo sau
a) \(\frac{\pi }{6}\);
b) \(\frac{{ - 5\pi }}{7}\);
c) \({270^0}\);
d) \( - {415^0}\).

Đường tròn lượng giác có tâm tại gốc tọa độ, bán kính bằng 1, lấy điểm A(1;0) là gốc của đường tròn.
Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \(\alpha \) là điểm M trên đường tròn lượng giác sao cho sđ(OA, OM) = \(\alpha \).

Advertisements (Quảng cáo)
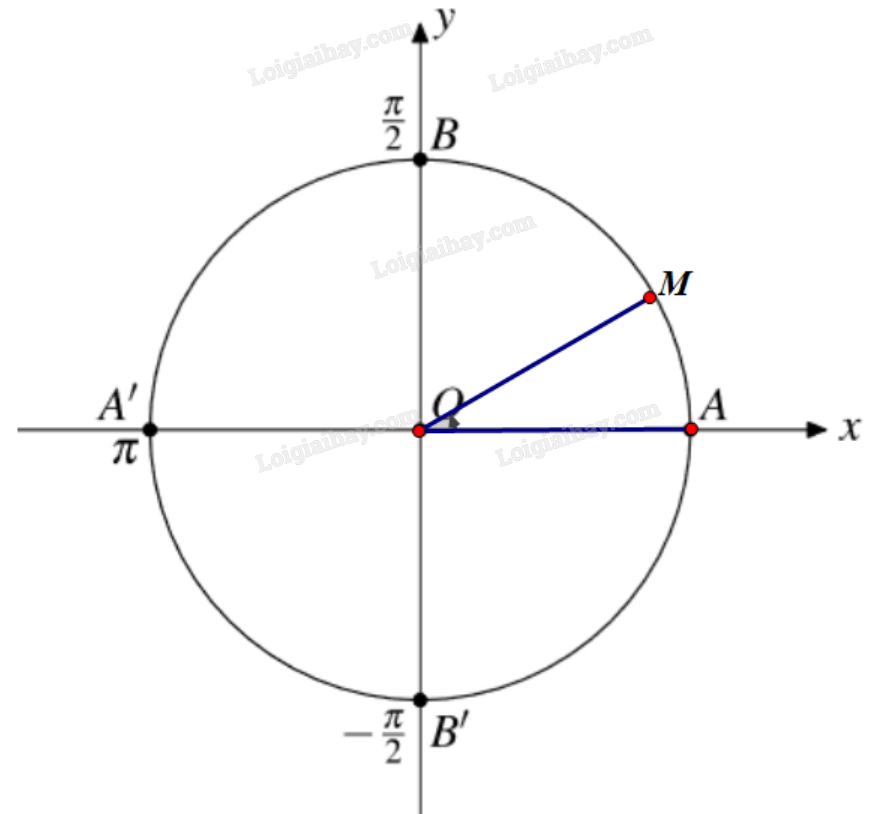
a) Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \(\frac{\pi }{6}\) được xác định như trên hình.
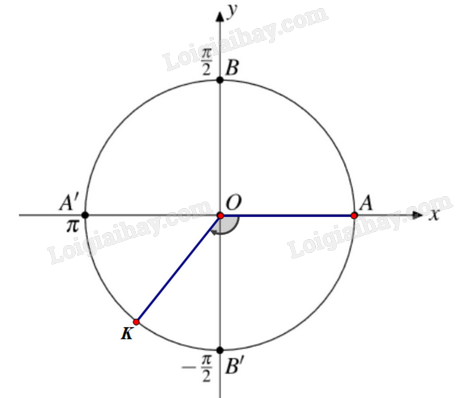
b) Điểm K trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \(\frac{{ - 5\pi }}{7}\) được xác định như trên hình.
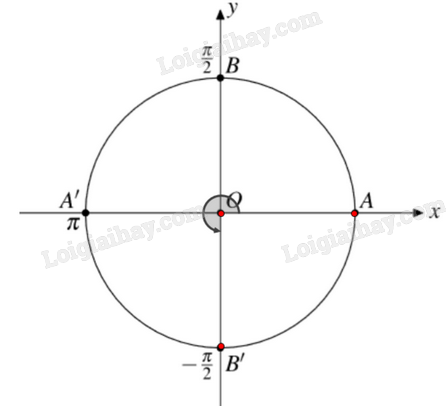
c) Điểm B’ trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \({270^0}\) được xác định như trên hình.
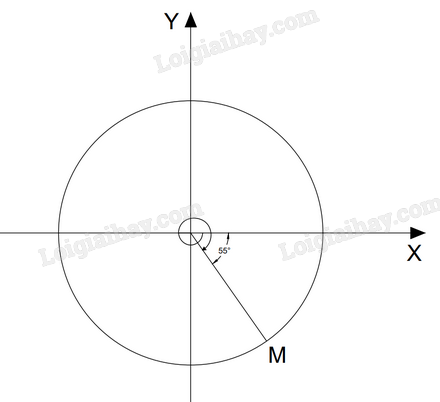
d) Để dễ dàng xác định góc hơn, ta tách \( - {415^0} = - {360^0} - {55^0}\).
Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \( - {415^0}\) được xác định như trên hình.