
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) \(y = \sin x - \cos x\);
b) \(y = \sin x + \sin \left( {\frac{\pi }{3} - x} \right)\);
c) \(y = {\sin ^4}x + {\cos ^4}x\)
d) \(y = \cos 2x + 2\cos x - 1\).

Áp dụng lý thuyết \( - 1 \le \sin x \le 1\), \( - 1 \le \cos x \le 1\), \(0 \le \left| {\cos x} \right| \le 1\), \(0 \le \left| {\sin x} \right| \le 1\), \(0 \le {\sin ^2}x \le 1\).

a) Ta có \(y = \sin x - \cos x = \sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right).\)
Vì \( - 1 \le \sin \left( {x - \frac{\pi }{4}} \right) \le 1\) nên \( - \sqrt 2 \le \sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right) \le \sqrt 2 \) với mọi \(x \in \mathbb{R}\).
Vậy giá trị lớn nhất của hàm số là \(\sqrt 2 \), đạt được khi
\(\sin \left( {x - \frac{\pi }{4}} \right) = 1 \Rightarrow x - \frac{\pi }{4} = \frac{\pi }{2} + k2\pi \Rightarrow x = \frac{{3\pi }}{4} + k2\pi .\)
Và giá trị nhỏ nhất của hàm số là \( - \sqrt 2 \), đạt được khi
\(\sin \left( {x - \frac{\pi }{4}} \right) = - 1 \Rightarrow x - \frac{\pi }{4} = - \frac{\pi }{2} + k2\pi \Rightarrow x = - \frac{\pi }{4} + k2\pi .\)
b) Ta có
\(\begin{array}{l}y = \sin x + \sin \left( {\frac{\pi }{3} - x} \right) = 2\sin \frac{{x + \left( {\frac{\pi }{3} - x} \right)}}{2}\cos \,\,\frac{{x - \left( {\frac{\pi }{3} - x} \right)}}{2}\\\,\,\,\, = 2\sin \frac{\pi }{6}\cos \left( {x - \frac{\pi }{6}} \right) = \cos \left( {x - \frac{\pi }{6}} \right)\end{array}\)
Vì \( - 1 \le \cos \left( {x - \frac{\pi }{6}} \right) \le 1\) với mọi \(x \in \mathbb{R}\).
Vậy giá trị lớn nhất của hàm số là 1, đạt được khi
Advertisements (Quảng cáo)
\(\cos \left( {x - \frac{\pi }{6}} \right) = 1 \Rightarrow x - \frac{\pi }{6} = k2\pi \Rightarrow x = \frac{\pi }{6} + k2\pi .\)
Và giá trị nhỏ nhất của hàm số là \( - 1\), đạt được khi
\(\cos \left( {x - \frac{\pi }{6}} \right) = - 1 \Rightarrow x - \frac{\pi }{6} = \pi + k2\pi \Rightarrow x = \frac{{7\pi }}{6} + k2\pi .\)
c) Ta có
\(\begin{array}{l}y = {\sin ^4}x + {\cos ^4}x = {\sin ^4}x + 2{\sin ^2}x.{\cos ^2}x + {\cos ^4}x - 2{\sin ^2}x.{\cos ^2}x\\\,\,\,\,\, = {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2} - 2{\sin ^2}x{\cos ^2}x = {1^2} - \frac{1}{2}.4{\sin ^2}x.{\cos ^2}x\\\,\,\,\,\, = 1 - \frac{1}{2}{\left( {2\sin x.\cos x} \right)^2} = 1 - \frac{1}{2}{\sin ^2}2x.\end{array}\)
Vì \(0 \le {\sin ^2}2x \le 1\) nên \(0 \le \frac{1}{2}{\sin ^2}2x \le \frac{1}{2}\) vì vậy \(\frac{1}{2} \le 1 - \frac{1}{2}{\sin ^2}2x \le 1\)với mọi \(x \in \mathbb{R}\).
Vậy giá trị lớn nhất của hàm số là \(1\), đạt được khi
\({\sin ^2}2x = 0 \Rightarrow \sin 2x = 0 \Rightarrow 2x = k\pi \Rightarrow x = k\frac{\pi }{4}.\)
Và giá trị nhỏ nhất của hàm số là \( - \sqrt 2 \), đạt được khi
\({\sin ^2}2x = 1 \Rightarrow \sin 2x = \pm 1 \Rightarrow 2x = \frac{\pi }{2} + k\pi \Rightarrow x = \frac{\pi }{4} + k\frac{\pi }{2}.\)
d) Ta có \(y = \cos 2x + 2\cos x - 1 = 2{\cos ^2}x - 1 + 2\cos x - 1 = 2{\cos ^2}x + 2\cos x - 2\)
Đặt \(t = \cos x\,\,( - 1 \le t \le 1)\) ta có hàm số \(y = 2{t^2} + 2t - 2\) trên đoạn \([ - 1;1]\) có đồ thị như sau
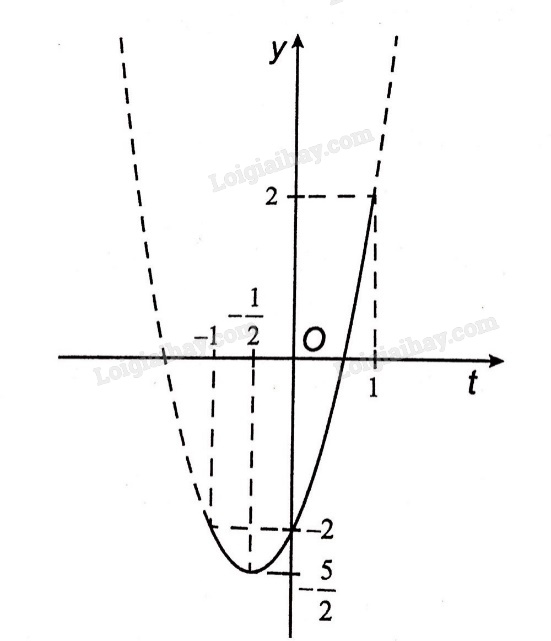
Dựa vào đồ thị, ta thấy:
Giá trị lớn nhất của hàm số là 2, đạt được khi t =1.
\(\cos x = 1 \Rightarrow x = k2\pi \)
Và giá trị nhỏ nhất của hàm số là \( - \frac{5}{2}\), đạt được khi \(t = - \frac{1}{2}\)
\(\cos x = - \frac{1}{2} \Rightarrow x = \pm \frac{{2\pi }}{3} + k2\pi \).
