
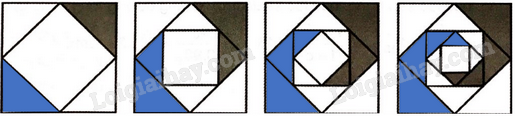
Các cạnh của hình vuông ban đầu có chiều dài 16cm. Một hình vuông mới được hình thành bằng cách nối các điểm giữa của các cạnh của hình vuông ban đầu và hai trong số các hình tam giác kết quả được tô màu (hình vẽ dưới). Nếu quá trình này được lặp lại năm lần nữa, hãy xác định tổng diện tích của vùng được tô màu.

+ Cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu là \({u_1}\) và công bội q thì số hạng tổng quát \({u_n}\) của nó được xác định bởi công thức \({u_n} = {u_1}.{q^{n - 1}}\) với \(n \ge 2\)
+ Cho cấp số nhân \(\left( {{u_n}} \right)\) với công bội \(q \ne 1\). Đặt \({S_n} = {u_1} + {u_2} + ... + {u_n}\). Khi đó, \({S_n} = \frac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}\)

Advertisements (Quảng cáo)
Gọi \({u_n}\) là diện tích hai tam giác được tô màu ở lần thực hiện thứ n. Gọi a là độ dài cạnh của hình vuông ban đầu.
Ở lần 1 thì độ dài cạnh tam giác vuông cân là \(\frac{a}{2}\) nên \({u_1} = 2.\frac{1}{2}.\frac{a}{2}.\frac{a}{2} = \frac{{{a^2}}}{{{2^2}}}\) và độ dài của cạnh hình vuông sau đó là \(\frac{{a\sqrt 2 }}{2}\)
Ở lần 2 thì độ dài cạnh tam giác vuông cân là \(\frac{a}{2}.\frac{{\sqrt 2 }}{2}\) nên \({u_2} = \frac{{{a^2}}}{{{2^3}}}\)
Ở lần 3 thì độ dài cạnh tam giác vuông cân là \(\frac{a}{2}.\frac{{\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2}\) nên \({u_3} = \frac{{{a^2}}}{{{2^4}}}\)’
Như vậy, dãy số (\({u_n}\)) là cấp số nhân với \({u_1} = \frac{{{a^2}}}{4}\) và công bội \(q = \frac{1}{2}\)
Vậy tổng diện tích sau năm lần thực hiện là \({S_5} = {u_1} = \frac{{1 - {q^5}}}{{1 - q}} = 124\left( {c{m^2}} \right)\)
