
Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD. Gọi M là một điểm bất kì thuộc cạnh SC.
a) Xác định giao tuyến của hai mặt phẳng (AMO) và (SCD).
b) Xác định giao tuyến của hai mặt phẳng (BMO) và (SCD).

Để xác định giao tuyến của hai mặt phẳng, ta tìm hai điểm chung (phân biệt) của hai mặt phẳng đó.

Advertisements (Quảng cáo)
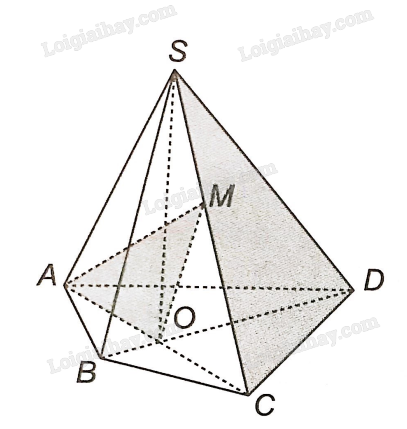
a) Ta thấy M thuộc AM, nằm trong mặt phẳng (AMO). M lại thuộc SC, nằm trong mặt phẳng (SCD). Vậy M là điểm chung thứ nhất của (AMO) và (SCD).
Ta thấy C thuộc đường thẳng AC (trùng với đường thẳng AO nên nó nằm trong mặt phẳng (AMO). C lại thuộc SC, nằm trong mặt phẳng (SCD). Vậy C là điểm chung thứ hai của (AMO) và (SCD).
Vậy nên MC (hay SC) là giao tuyến của hai mặt phẳng (AMO) và (SCD).
b) Ta thấy M thuộc BM, nằm trong mặt phẳng (BMO). M lại thuộc SC, nằm trong mặt phẳng (SCD). Vậy M là điểm chung thứ nhất của (BMO) và (SCD).
Ta thấy D thuộc đường thẳng BD (trùng với đường thẳng BO nên nó nằm trong mặt phẳng (BMO). D lại thuộc SD, nằm trong mặt phẳng (SCD). Vậy D là điểm chung thứ hai của (BMO) và (SCD).
Vậy nên MD là giao tuyến của hai mặt phẳng (BMO) và (SCD).
