
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD.
a) Xác định giao tuyến của hai mặt phẳng (SAM) và (SCD).
b) Xác định giao tuyến của hai mặt phẳng (SBN) và (SAD).
c) Xác định giao tuyến của hai mặt phẳng (SAM) và (SBN).

Để xác định giao tuyến của hai mặt phẳng, ta tìm hai điểm chung (phân biệt) của hai mặt phẳng đó.

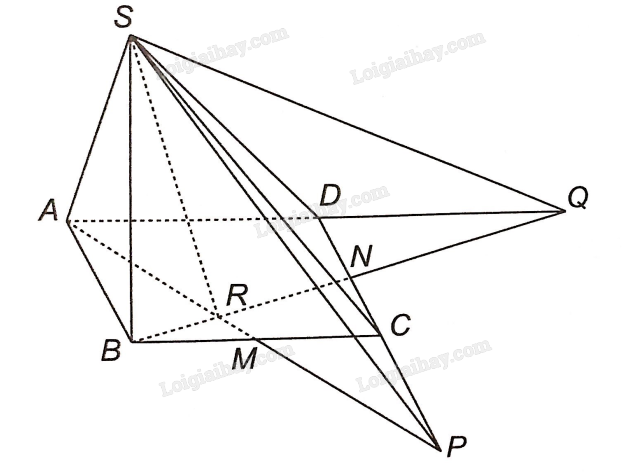
Advertisements (Quảng cáo)
a) Ta thấy S là điểm chung thứ nhất của hai mặt phẳng (SAM) và (SCD).
Trong mặt phẳng (ABCD): Gọi P là giao điểm của AM và CD => P là điểm chung thứ hai của mặt phẳng (SAM) và (SCD).
Vậy SP là giao tuyến của (SAM) và (SCD).
b) Ta thấy S là điểm chung thứ nhất của hai mặt phẳng (SBN) và (SAD).
Trong mặt phẳng (ABCD): Gọi Q là giao điểm của AM và CD => P là điểm chung thứ hai của mặt phẳng (SBN) và (SAD).
Vậy SQ là giao tuyến của (SBN) và (SAD).
c) Ta thấy S là điểm chung thứ nhất của hai mặt phẳng (SAM) và (SBN).
Trong mặt phẳng (ABCD): Gọi R là giao điểm của AM và BN => R là điểm chung thứ hai của mặt phẳng (SAM) và (SBN).
Vậy SR là giao tuyến của (SAM) và (SBN).
