
Cho tứ diện ABCD. Một mặt phẳng cắt bốn cạnh AB, BC, CD, DA lần lượt tại các điểm M, N, P, Q.
a) Chứng minh rằng các đường thẳng MN, PQ, AC đôi một song song hoặc đồng quy.
b) Chứng minh rằng các đường thẳng MQ, NP, BD đôi một song song hoặc đồng quy.

Dựa vào định lý về 3 đường giao tuyến của 3 mặt phẳng: Nếu có 2 giao tuyến của song song với nhau thì giao tuyến thứ 3 cũng song song với 2 giao tuyến đó. Còn nếu có 2 giao tuyến cắt nhau thì 3 giao tuyến đó đồng quy.

a)
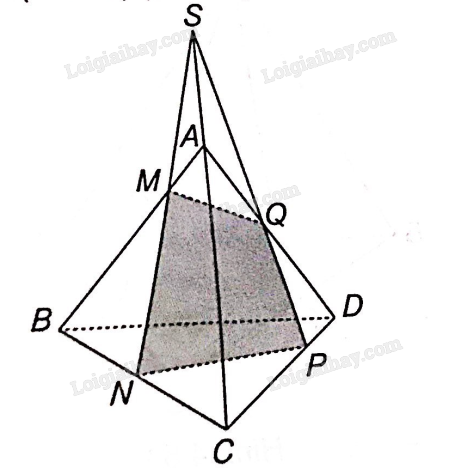
Xét 3 mặt phẳng (ABC), (ACD) và (MNPQ)
MN là giao tuyến của (MNPQ) và (ABC)
Advertisements (Quảng cáo)
PQ là giao tuyến của (MNPQ) và (ACD)
AC là giao tuyến của (ABC) và (ACD).
Vậy, theo tính chất 3 giao tuyến của 3 mặt phẳng cắt nhau thì các đường thẳng MN, PQ, AC đôi một song song hoặc đồng quy.
b)
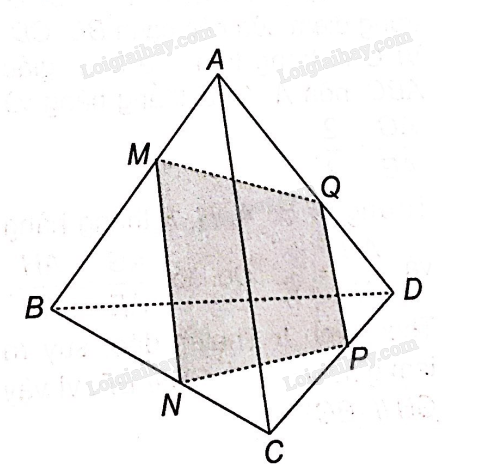
Xét 3 mặt phẳng (ABD), (BCD) và (MNPQ)
MQ là giao tuyến của (MNPQ) và (ABD)
NP là giao tuyến của (MNPQ) và (BCD)
BD là giao tuyến của (ABD) và (BCD).
Vậy, theo tính chất 3 giao tuyến của 3 mặt phẳng cắt nhau thì các đường thẳng MQ, NP, BD đôi một song song hoặc đồng quy.
