
Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường a, b, c, d đôi một song song và không nằm trong mặt phẳng (ABCD).
a) Chứng minh rằng hai mặt phẳng mp(a,b) và mp(c,d) song song với nhau.
b) Chứng minh rằng hai mặt phẳng mp(a,d) và mp(b,c) song song với nhau.
c) Một mặt phẳng cắt bốn đường thẳng a, b, c, d lần lượt tại A’, B’, C’, D’. Chứng minh rằng tứ giác A’B’C’D’ là hình bình hành.

Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng \(\left( \beta \right)\) thì \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.

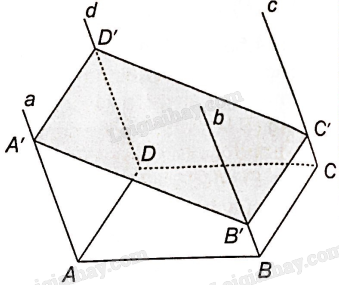
a) Vì a//d nên a//mp(c, d).
Advertisements (Quảng cáo)
Vì ABCD là hình bình hành nên AB//CD, do đó AB// mp(c, d).
Mặt phẳng (a, b) chứa hai đường thẳng a và AB cắt nhau tại A và cùng song song với mp(c, d).
Do đó, hai mặt phẳng mp(a,b) và mp(c,d) song song với nhau.
b) Vì a//b nên a//mp(b, c).
Vì ABCD là hình bình hành nên AD//BC, do đó AD// mp(b, c).
Mặt phẳng (a, d) chứa hai đường thẳng a và AD cắt nhau tại A và cùng song song với mp(b, c).
hai mặt phẳng mp(a,d) và mp(b,c) song song với nhau.
c) Vì mặt phẳng (a, b) song song với mặt phẳng (c, d) nên giao tuyến của mặt phẳng (A’B’C’D’) với hai mặt phẳng đó song song với nhau, tức là A’B’//C’D’.
Vì hai mặt phẳng mp(a,d) và mp(b,c) song song với nhau nên giao tuyến của mặt phẳng (A’B’C’D’) với hai mặt phẳng đó song song với nhau, tức là A’D’//C’B’.
Tứ giác A’B’C’D’ có: A’B’//C’D’, A’D’//C’B’ nên tứ giác A’B’C’D’ là hình bình hành.
