Cho hình hộp ABCD.A’B’C’D’.
a) Xác định giao tuyến d của hai mặt phẳng (ADC’B’) và (A’D’CB).
b) Chứng minh rằng d // AD.
c) Chứng minh rằng d đi qua trung điểm của các đường chéo của hình hộp.
Đường thẳng chung d (nếu có) của hai mặt phẳng phân biệt (P) và (Q) được gọi là giao tuyến của hai mặt phẳng đó.
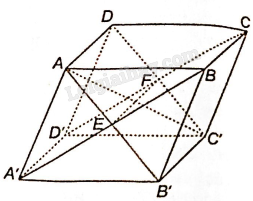
a) Gọi E là giao điểm của AB’ và A’B; gọi F là giao điểm của CD’ và C’D. Vì đường thẳng EF vừa thuộc cả hai mặt phẳng (ADC’B’) và (A’D’CB) nên EF là giao tuyến của hai mặt phẳng (ADC’B’) và (A’D’CB).
b) Hai mặt phẳng (ADC’B’) và (A’D’CB) chứa hai đường thẳng song song là AD và BC nên giao tuyến EF của hai mặt phẳng đó song song với AD.
c) Tứ giác ABCD và BCC’B’ là hình bình hành nên AD//BC, \(AD = BC\) và BC//B’C’ và \(BC = B’C’\), do đó ADC’B’ là hình bình hành.
Vì E, F lần lượt là trung điểm của AB’ và CD’ nên EF đi qua trung điểm của AC’. Vì các đường chéo của hình hộp cùng đi qua trung điểm của mỗi đường nên đường thẳng EF đi qua trung điểm các đường chéo đó.