
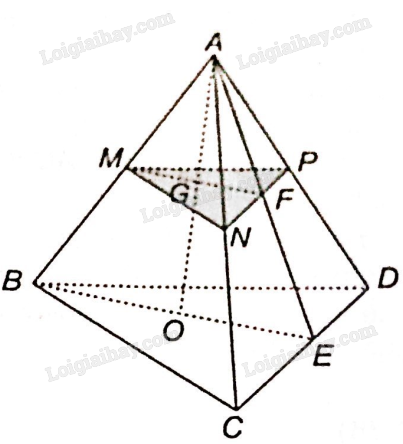
Cho tứ diện ABCD và các điểm M, N, P lần lượt thuộc các cạnh AB, AC, AD. Gọi O là một điểm nằm trong tam giác BCD.
a) Xác định giao tuyến của hai mặt phẳng (ABO) và (ACD).
b) Xác định giao tuyến của hai mặt phẳng (ABO) và (MNP).
c) Xác định giao điểm của đường thẳng AO và mặt phẳng (MNP).

Để xác định giao tuyến của hai mặt phẳng, ta tìm hai điểm chung (phân biệt) của hai mặt phẳng đó.

Advertisements (Quảng cáo)
a) Ta thấy A là điểm chung đầu tiên của hai mặt phẳng (ABO) và (ACD).
Trong mặt phẳng (BCD): Gọi E là giao điểm của BO và CD. Vậy E là điểm chung thứ hai của hai mặt phẳng (ABO) và (ACD).
Vậy giao tuyến của hai mặt phẳng (ABO) và (ACD) là đường thẳng AE.
b) Ta thấy M thuộc AB, nằm trong mặt phẳng (ABO) vậy M là điểm chung thứ nhất của hai mặt phẳng (ABO) và (MNP).
Trong mặt phẳng (BCD): gọi E là giao điểm của BO và CD.
Trong mặt phẳng (ACD): gọi F là giao điểm của NP và AE. Vậy F là điểm chung thứ hai của (MNP) và (ABO).
Vậy giao tuyến của hai mặt phẳng (ABO) và (MNP) là đường thẳng MF.
c) Trong mặt phẳng (ABE) gọi G là giao điểm của AO và MF.
Vậy giao điểm của đường thẳng AO và mặt phẳng (MNP) là điểm G.
