
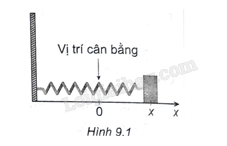
Một vật gắn trên lò xo chuyển động theo phương ngang trên một mặt phẳng nhẵn (H.9.1). Phương trình chuyển động của vật được cho bởi \(x = 8\sin \left( {\sqrt 2 \pi t + \frac{\pi }{3}} \right)\), với \(t\) tính bằng giây và \(x\) tính bằng centimét. Tìm vận tốc và gia tốc của vật tại thời điểm \(t = 5\) giây (làm tròn kết quả đến chữ số thập phân thứ nhất). Vật chuyển động theo hướng nào tại thời điểm đó?’

Vận tốc và gia tốc của vật tại thời điểm \(t\) là:
\(v\left( t \right) = x’\left( t \right)\)
\(a\left( t \right) = x”\left( t \right)\)
Advertisements (Quảng cáo)
Tại \(t = 5\) giây, tính vận tốc và gia tốc của vật là \(v\) và \(a\).

Vận tốc và gia tốc của vật tại thời điểm \(t\) là:
\(v\left( t \right) = x’\left( t \right) = 8\pi \sqrt 2 {\rm{cos}}\left( {\sqrt 2 \pi t + \frac{\pi }{3}} \right)\)
\(a\left( t \right) = x”\left( t \right) = - 16{\pi ^2}\sin \left( {\sqrt 2 \pi t + \frac{\pi }{3}} \right)\)
Tại \(t = 5\) giây, vận tốc và gia tốc của vật là \(v = - 10,5{\rm{\;m}}/{\rm{s}}\) và \(a = 150,8{\rm{\;m}}/{{\rm{s}}^2}\). Khi ấy vật đang chuyển động theo hướng từ phải sang trái (hướng tới vách chắn cố định).
