Hãy xác định tọa độ các đỉnh của tam giác A’B’C’ và phương trình của đường thẳng d theo thứ tự là ảnh của tam giác ABC và đường thẳng d qua phép quay tâm O, góc quay 90°.. Bài 1.16 trang 26 Sách bài tập (SBT) Hình học 11 - Bài 5. Phép quay
Trong mặt phẳng Oxy cho các điểm A(3; 3), B(0; 5), C(1; 1) và đường thẳng d có phương trình \(5x - 3y + 15 = 0\). Hãy xác định tọa độ các đỉnh của tam giác A’B’C’ và phương trình của đường thẳng d theo thứ tự là ảnh của tam giác ABC và đường thẳng d qua phép quay tâm O, góc quay 90°.
Giải:
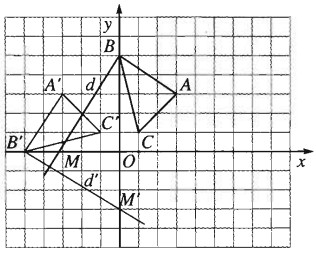
Gọi \({Q_{\left( {0;90^\circ } \right)}}\) là phép quay tâm O, góc quay 90°.
\(A’\left( { - 3;3} \right)\)
Advertisements (Quảng cáo)
\(B’\left( {5;0} \right)\)
\(C’\left( { - 1;1} \right)\)
d đi qua B và \(M\left( { - 3;0} \right)\)
\(M’ = {Q_{\left( {0;90^\circ } \right)}};M = \left( {0; - 3} \right)\) nên d’ là đường thẳng B’M’ có phương trình \(3x + 5y + 15 = 0\)