Viết phương trình đường thẳng d’ là ảnh của d qua phép đối xứng tâm. Bài 1.43 trang 40 Sách bài tập (SBT) Hình học 11 - Đề toán tổng hợp Chương I
Trong mặt phẳng Oxy cho đường thẳng \(d:2x - y + 6 = 0\). Viết phương trình đường thẳng d’ là ảnh của d qua phép đối xứng tâm \(I\left( { - 2;1} \right)\).
Dùng công thức tọa độ của phép đối xứng tâm \(I\left( { - 2;1} \right)\), ta có:
\(M’ = {D_1}\left( M \right)\)
\(\Rightarrow M’\left\{ \matrix{
x’ = 2.\left( { - 2} \right) - x \hfill \cr
y’ = 2.1 - y \hfill \cr} \right.\)
Advertisements (Quảng cáo)
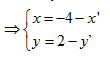
Thế \(\left( {x;y} \right)\) vào phương trình d, ta có phương trình
\(\eqalign{
& d’:2\left( { - 4 - x’} \right) - \left( {2 - y’} \right) + 6 = 0 \cr
& \Rightarrow d’:2{\rm{x}}’ - y’ + 4 = 0 \cr} \). Đổi kí hiệu, ta có phương trình:
\(d’:2{\rm{x}} - y + 4 = 0\)