Advertisements (Quảng cáo)
Cho hàm số
\(f\left( x \right) = \left\{ \matrix{
{x^2}{\rm{ ,\,\, nếu }}\,\,x \ge 0 \hfill \cr
{x^2} – 1,\,\,{\rm{ nếu }}\,\,x < 0 \hfill \cr} \right.\)
a) Vẽ đồ thị của hàm số \(f\left( x \right)\). Từ đó dự đoán về giới hạn của \(f\left( x \right)\) khi \(x \to 0\)
b) Dùng định nghĩa chứng minh dự đoán trên.
Giải:
\(f\left( x \right) = \left\{ \matrix{
{x^2}{\rm{ ,\,\, nếu }}\,\,x \ge 0 \hfill \cr
{x^2} – 1,\,\,{\rm{ nếu }}\,\,x < 0 \hfill \cr} \right.\)
a) (H.6) Dự đoán : Hàm số \(f\left( x \right)\) không có giới hạn khi \(x \to 0\)
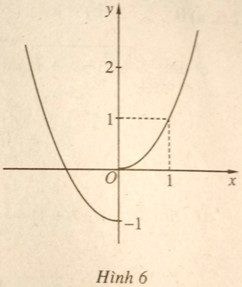
Advertisements (Quảng cáo)
b) Lấy hai dãy số có số hạng tổng quát là \({a_n} = {1 \over n}\) và \({b_n} = – {1 \over n}\)
Ta có, \({a_n} \to 0\) và \({b_n} \to 0\) khi \(n \to + \infty \) (1)
Vì \({1 \over n} > 0\) nên \(f\left( {{a_n}} \right) = {1 \over {{n^2}}}\)
Do đó, \(\mathop {\lim }\limits_{n \to + \infty } f\left( {{a_n}} \right) = \mathop {\lim }\limits_{n \to + \infty } {1 \over {{n^2}}} = 0\) (2)
Vì \( – {1 \over n} < 0\) nên \(f\left( {{b_n}} \right) = {1 \over {{n^2}}} – 1\)
Do đó, \(\mathop {\lim }\limits_{n \to + \infty } f\left( {{b_n}} \right) = \mathop {\lim }\limits_{n \to + \infty } \left( {{1 \over {{n^2}}} – 1} \right) = – 1\) (3)
Từ (1), (2) và (3) suy ra \(f\left( x \right)\) không có giới hạn khi \(x \to 0\)