Cho tứ diện ABCD. Gọi I và J lần lượt là hai điểm di động trên các cạnh AD và BC sao cho \({{IA} \over {I{\rm{D}}}} = {{JB} \over {JC}}\). Chứng minh rằng IJ luôn luôn song song với một mặt phẳng cố định.

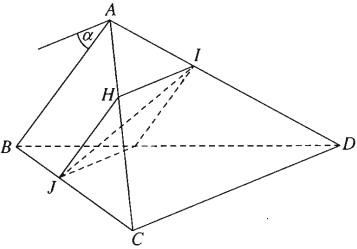
Qua I kẻ đường thẳng song song với CD cắt AC tại H, ta có:
\({{HA} \over {HC}} = {{IA} \over {I{\rm{D}}}}\)
Mặt khác \({{IA} \over {I{\rm{D}}}} = {{JB} \over {JC}}\)
Advertisements (Quảng cáo)
Nên \({{HA} \over {HC}} = {{JB} \over {JC}}\)
Suy ra \(HJ\parallel AB\)
Như vậy mặt phẳng (IJH) song song với AB và CD.
Gọi \(\left( \alpha \right)\) là mặt phẳng qua AB và song song với CD, ta có
\(\left\{ \matrix{
\left( \alpha \right)\parallel \left( {IJH} \right) \hfill \cr
IJ \subset \left( {IJH} \right) \hfill \cr} \right. \Rightarrow IJ\parallel \left( \alpha \right)\)
Vậy IJ song song với mặt phẳng \(\left( \alpha \right)\) cố định.
