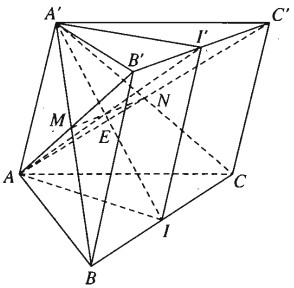
Cho hình lăng trụ tam giác ABCA’B’C’ có các cạnh bên là AA’, BB’, CC’. Gọi I và I’tương ứng là trung điểm của hai cạnh BC và B’C’.
a) Chứng minh rằng \(AI\parallel A’I’\).
b) Tìm giao điểm của IA’ với mặt phẳng (AB’C’).
c) Tìm giao tuyến của (AB’C’) và (A’BC).

a) Ta có \(II’\parallel BB’\) và II’ = BB’
Mặt khác \(AA’\parallel BB’\) và AA’ = BB’ nên :
\(AA’\parallel II’\) và AA’ = II’
⇒ AA’II’ là hình bình hành.
\( \Rightarrow AI\parallel A’I’\)
b) Ta có:
\(\left\{ \matrix{
A \in \left( {AB’C’} \right) \hfill \cr
A \in \left( {AA’I’I} \right) \hfill \cr} \right.\)
Advertisements (Quảng cáo)
\( \Rightarrow A \in \left( {AB’C’} \right) \cap \left( {AA’I’I} \right)\)
Tương tự :
\(\left\{ \matrix{
I’ \in B’C` \hfill \cr
I’ \in \left( {AA’I’I} \right) \hfill \cr} \right. \Rightarrow I’ \in \left( {AB’C’} \right)\)
\(I’ \in \left( {AB’C’} \right) \cap \left( {AA’I’I} \right) \Rightarrow \left( {AB’C’} \right) \cap \left( {AA’I’I} \right) = AI’\)
Đặt \(AI’ \cap A’I = E\). Ta có:
\(\left\{ \matrix{E \in IA` \hfill \cr E \in AI` \hfill \cr} \right. \Rightarrow E \in \left( {AB’C’} \right)\)
Vậy E là giao điểm của AI’ và mặt phẳng (AB’C’)
c) Ta có:
\(A’B \cap AB’ = M \Rightarrow \left\{ \matrix{
M \in \left( {AB’C’} \right) \hfill \cr
M \in \left( {A’BC} \right) \hfill \cr} \right.\)
Tương tự:
\(AC’ \cap A’C = N \Rightarrow \left\{ \matrix{
N \in \left( {AB’C’} \right) \hfill \cr
N \in \left( {A’BC} \right) \hfill \cr} \right.\)
Vậy \(\left( {AB’C’} \right) \cap \left( {A’BC} \right) = MN\).
