Trong mặt phẳng \(\left( \alpha \right)\) cho tam giác ABC. Từ ba đỉnh của tam giác này ta kẻ các nửa đường thẳng song song cùng chiều Ax, By, Cz không nằm trong \(\left( \alpha \right)\). Trên Ax lấy đoạn AA’ = a, trên By lấy đoạn BB’ = b, trên Cz lấy đoạn CC’ = c.
a) Gọi I, J và K lần lượt là các giao điểm B’C’, C’A’ và A’B’ với \(\left( \alpha \right)\).
Chứng minh rằng \({{IB} \over {IC}}.{{JC} \over {J{\rm{A}}}}.{{K{\rm{A}}} \over {KB}} = 1\)
b) Gọi G và G’ lần lượt là trọng tâm của các tam giác ABC và A’B’C’.
Chứng minh: \(GG’\parallel AA’\).
c) Tính GG’ theo a, b, c

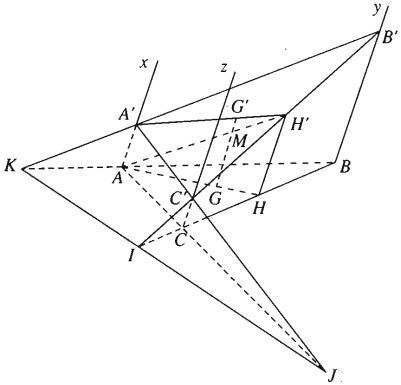
a) \(CC’\parallel BB’ \Rightarrow \Delta ICC’ \sim \Delta IBB’\)
\( \Rightarrow {{IB} \over {IC}} = {{BB’} \over {CC’}} = {b \over c}\)
\(CC’\parallel AA’ \Rightarrow \Delta JCC’ \sim \Delta JAA’\)
\( \Rightarrow {{JC} \over {JA}} = {{CC’} \over {AA’}} = {c \over a}\)
\(AA’\parallel BB’ \Rightarrow \Delta KAA’ \sim \Delta KBB’\)
\( \Rightarrow {{KA} \over {KB}} = {{AA’} \over {BB’}} = {a \over b}\)
Advertisements (Quảng cáo)
Do đó: \({{IB} \over {IC}}.{{JC} \over {J{\rm{A}}}}.{{K{\rm{A}}} \over {KB}} = {b \over c}.{c \over a}.{a \over b} = 1\)
b) Gọi H và H’ lần lượt là trung điểm của các cạnh BC và B’C’. Vì HH’ là đường trung bình của hình thang BB’CC’ nên \(HH’\parallel BB’\).
Mà \(BB’\parallel AA’\) suy ra \(HH’\parallel AA’\)
Ta có: \(G \in AH\) và \(G’ \in A’H’\) và ta có:
\(\left\{ \matrix{
{{AG} \over {AH}} = {2 \over 3} \hfill \cr
{{A’G’} \over {A’H’}} = {2 \over 3} \hfill \cr} \right. \Rightarrow AA’\parallel GG’\parallel HH’\)
c) \(AH’ \cap GG’ = M \Rightarrow GG’ = G’M + MG\)
Ta có: \(G’M\parallel AA’ \Rightarrow \Delta H’G’M \sim \Delta H’A’A\)
\( \Rightarrow {{G’M} \over {AA’}} = {{H’G’} \over {H’A’}} = {1 \over 3} \Rightarrow G’M = {1 \over 3}AA’ = {1 \over 3}a\)
\(MG\parallel HH’ \Rightarrow \Delta AMG \sim \Delta AH’H\)
\( \Rightarrow {{MG} \over {HH’}} = {{AG} \over {AH}} = {2 \over 3} \Rightarrow MG = {2 \over 3}HH’\)
Mặt khác HH’ là đường trung bình của hình thang BB’CC’ nên
\(HH’ = {{BB’ + CC’} \over 2} = {{b + c} \over 2} \Rightarrow MG = {2 \over 3}HH’ = {2 \over 3}.{{b + c} \over 2} = {1 \over 3}\left( {b + c} \right)\)
Do đó: \(GG’ = G’M + MG = {1 \over 3}a + {1 \over 3}\left( {b + c} \right) = {1 \over 3}\left( {a + b + c} \right)\)
Vậy \(GG’ = {1 \over 3}\left( {a + b + c} \right)\).
