Từ các đỉnh của tam giác ABC ta kẻ các đoạn thẳng AA’, BB’, CC’ song song cùng chiều, bằng nhau và không nằm trong mặt phẳng của tam giác. Gọi I, G và K lần lượt là trọng tâm của các tam giác ABC, ACC’, A’B’C’.
a) Chứng minh \(\left( {IGK} \right)\parallel \left( {BB’CC’} \right)\).
b) Chứng minh rằng \(\left( {A’GK} \right)\parallel \left( {AIB’} \right)\).

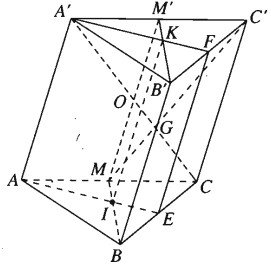
Gọi M và M’ tương ứng là trung điểm của AC và A’C’, ta có:
\(I \in BM,G \in C’M,K \in B’M’\)
Theo tính chất trọng tâm của tam giác ta có:
Advertisements (Quảng cáo)
\({{MI} \over {MB}} = {{MG} \over {MC’}} = {1 \over 3} \Rightarrow IG\parallel BC’\);
\({{MI} \over {MB}} = {{M’K} \over {M’B’}} = {1 \over 3}\) và \(MM’\parallel BB’ \Rightarrow IK\parallel BB’\)
Ta có :
\(\left\{ \matrix{
IG\parallel BC` \hfill \cr
BC’ \subset \left( {BB’C’C} \right) \hfill \cr} \right. \Rightarrow IG\parallel \left( {BB’C’C} \right)\)
\(\left\{ \matrix{
IK\parallel BB` \hfill \cr
BB’ \subset \left( {BB’C’C} \right) \hfill \cr} \right. \Rightarrow IK\parallel \left( {BB’C’C} \right)\)
Mặt khác IG và \(IK \subset \left( {IGK} \right)\) nên \(\left( {IGK} \right)\parallel \left( {BB’C’C} \right)\)
b) Gọi E và F tương ứng là trung điểm của BC và B’C’, O là trung điểm của A’C. A, I, E thẳng hàng nên (AIB’) chính là (AEB’). A’, G, C thẳng hàng nên (A’GK) chính là (A’CF).
Ta có \(B’E\parallel CF\) (do B’FCE là hình bình hành ) và \(AE\parallel A’F\) nên \(\left( {AIB’} \right)\parallel \left( {A’GK} \right)\).
