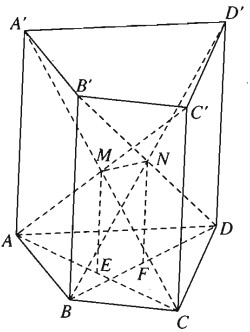
Cho hình lăng trụ tứ giác ABCD.A’B’C’D’.
a) Chứng minh rằng hai đường chéo AC’ và A’C cắt nhau và hai đường chéo BD’ và B’Dcắt nhau.
b) Cho E và F lần lượt là trung điểm của hai đường chéo AC và BD.Chứng minh MN = EF.

Advertisements (Quảng cáo)
Hình bình hành ACC’A có hai đường chéo là
AC’ và A’C cắt nhau tại trung điểm Mcủa mỗi đường. Tương tự, hai đường chéo BD’ và B’D cắt nhau tại trung điểm N của mỗi đường.
b) Trung điểm E của AC là hình chiếu của trung điểm M của AC’ thep phương của cạnh lăng trụ. Tương tự, trung điểm F là hình chiếu trung điểm N của đường chéo BD’ trên BD. Ta có \(EM\parallel CC’\) và \(EM = {{CC’} \over 2}\)
Mặt khác \(FN\parallel DD’\) và \(FN = {{DD’} \over 2}\). Từ đó suy ra tứ giác MNFE là hình bình hành và ta có MN = EF.
