Cho hình chóp S.ABCD có đáy là hình thang ( đáy lớn AD). Gọi O la giao điểm của ACvà BD, I và J lần lượt là trung điểm của SB và SC.
a) Xác định giao điểm M của AI và (SCD).
b) Chứng minh \(IJ\parallel \left( {SAD} \right)\).
c) Xác định thiết diện của hình chóp cắt bởi mp (P) qua I, song song với SD và AC.

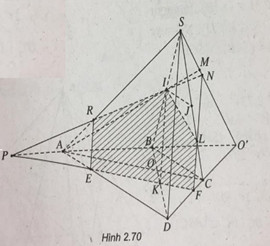
a) Gọi \(O’ = AB \cap C{\rm{D}},M = AI \cap SO’\)
Ta có: \(M = AI \cap \left( {SC{\rm{D}}} \right)\)
Advertisements (Quảng cáo)
b)
\(\eqalign{
& IJ\parallel BC \Rightarrow IJ\parallel AD \cr
& \Rightarrow IJ\parallel \left( {SAD} \right) \cr} \)
c) 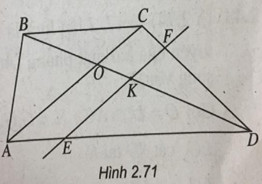
Đường thẳng qua I song song với SD cắt BD tại K. Do \({{OB} \over {O{\rm{D}}}} = {{BC} \over {A{\rm{D}}}} < 1\) nên OB < OD. Do đó điểm K thuộc đoạn OD.
Qua K, kẻ đường thẳng song song với AC cắt DA, DC, BA lần lượt tại E, F, P.
Gọi \(R = IP \cap SA\). Kéo dài PI cắt SO’ tại N
Gọi \(L = NF \cap SC\)
Ta có thiết diện là ngũ giác IREFL.
