Cho hình lập phương ABCD.A’B’C’D’ các trung điểm E, F của các cạnh AB, DD’. Hãy xác định các thiết diện của hình lập phương cắt bởi các mặt phẳng (EFB), (EFC), (EFC’) và (EFK) với K là trung điểm của cạnh B’C’.

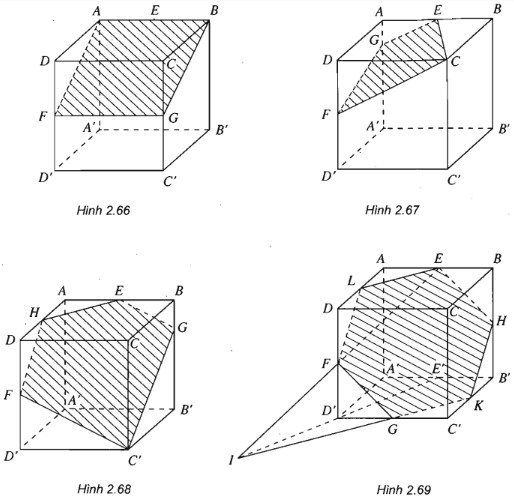
Ta xác định thiết diện của hình lập phương cắt bởi các mặt phẳng sau:
- Mặt phẳng (EFB): ta vẽ \(FG\parallel AB\) và được thiết diện là hình chữ nhật ABGF, G là trung điểm của CC’.
Advertisements (Quảng cáo)
- (h.2.67) Mặt phẳng (EFC): Nối FC và vẽ \(EG\parallel FC\), ta được thiết diện là hình thang \(ECFG\left( {AG = {1 \over 4}AA’} \right)\).
- (h.2.68) Mặt phẳng (EFC’): Nối FC’ và vẽ \(EG\parallel FC’\). Nối GC’ và vẽ \(FH\parallel GC’\). Ta được thiết diện là hình ngũ giác EGC’FH.
\(\left( {BG = {1 \over 4}BB’,AH = {1 \over 3}A{\rm{D}}} \right)\)
- (h.2.69) Mặt phẳng (EFK) với K là trung điểm của đoạn B’C’. Lấy trung điểm E’ của đoạn A’B’. Ta có \(I = EF \cap E’D’\). Ta có IK là giao tuyến của hai mặt phẳng (EFK) và (A’B’C’D’). Gọi \(G = IK \cap C’D’\). Nối F với G, vẽ \(EH\parallel FG\). Nối K với H, vẽ \(FL\parallel KH\) và nối L với E. Ta được thiết diện là hình lục giác đều EHKGFL. (G, H, L theo thứ tự là trung điểm của D’C’, B’B, AD).
