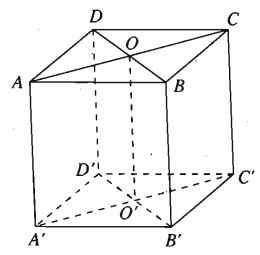
Cho hình lập phương ABCDA’B’C’D’ cạnh a. Gọi O và O’ theo thứ tự là tâm của hai hình vuông ABCD và A’B’C’D’.
a) Hãy biểu diễn các vectơ \(\overrightarrow {AO} ,\overrightarrow {AO’} \) theo các vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho.
b) Chứng minh rằng \(\overrightarrow {A{\rm{D}}} + \overrightarrow {D’C’} + \overrightarrow {D’A’} = \overrightarrow {AB} \).

a) *\(\overrightarrow {AO} = {1 \over 2}\overrightarrow {AC} = {1 \over 2}\overrightarrow {A’C’} = {1 \over 2}\left( {\overrightarrow {AB} + \overrightarrow {A{\rm{D}}} } \right)\)
Advertisements (Quảng cáo)
\(\overrightarrow {AO} = \overrightarrow {AB} + \overrightarrow {BO} = \overrightarrow {AB} + {1 \over 2}\overrightarrow {B{\rm{D}}} ,v.v....\)
*\(\overrightarrow {AO} = {1 \over 2}\overrightarrow {AC} + \overrightarrow {AA’} \)
\(\eqalign{
& = {1 \over 2}\left( {\overrightarrow {AA’} + \overrightarrow {AC’} } \right) = {1 \over 2}\left( {\overrightarrow {AB’} + \overrightarrow {AD’} } \right) \cr
& = \overrightarrow {AA’} + \overrightarrow {A’B’} + {1 \over 2}\overrightarrow {B’D’} \cr
& = \overrightarrow {AB} + \overrightarrow {BB’} + {1 \over 2}\overrightarrow {B’D’} ,v.v... \cr} \)
b) \(\overrightarrow {AD} + \overrightarrow {D’C’} + \overrightarrow {D’A’} = \overrightarrow {AD} + \overrightarrow {DC} + \overrightarrow {CB} \)
(vì \(\overrightarrow {D’C’} = \overrightarrow {DC} \) và \(\overrightarrow {D’A’} = \overrightarrow {CB} \)) nên \(\overrightarrow {A{\rm{D}}} + \overrightarrow {D’C’} + \overrightarrow {D’A’} = \overrightarrow {AB} \).
