Trên mặt phẳng \(\left( \alpha \right)\) cho hình bình hành \({A_1}{B_1}{C_1}{D_1}\). Về một phía đối với mặt phẳng \(\left( \alpha \right)\) ta dựng hình bình hành \({A_2}{B_2}{C_2}{D_2}\). Trên các đoạn \({A_1}{A_2},{B_1}{B_2},{C_1}{C_2},{D_1}{D_2}\) ta lần lượt lấy các điểm A, B, C, D sao cho
\({{A{A_1}} \over {A{A_2}}} = {{B{B_1}} \over {B{B_2}}} = {{C{C_1}} \over {C{C_2}}} = {{D{D_1}} \over {D{D_2}}} = 3\)
Chứng minh rằng tứ giác ABCD là hình bình hành

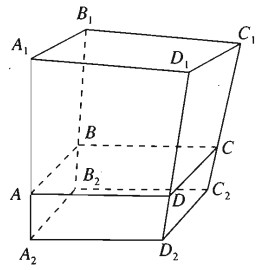
Lấy điểm O cố định rồi đặt \(\overrightarrow {O{A_1}} = \overrightarrow {{a_1}} ,\,\,\overrightarrow {O{B_1}} = \overrightarrow {{b_1}} ,\,\,\overrightarrow {O{C_1}} = \overrightarrow {{c_1}} ,\,\,\overrightarrow {O{D_1}} = \overrightarrow {{d_1}} \). Điều kiện cần và đủ để tứ giác \({A_1}{B_1}{C_1}{D_1}\) là hình bình hành là \(\overrightarrow {{a_1}} + \overrightarrow {{c_1}} = \overrightarrow {{b_1}} + \overrightarrow {{d_1}} \) ( theo bài tập 3.2) (1)
Đặt \(\overrightarrow {O{A_2}} = \overrightarrow {{a_2}} ,\overrightarrow {O{B_2}} = \overrightarrow {{b_2}} ,\overrightarrow {O{C_2}} = \overrightarrow {{c_2}} ,\overrightarrow {O{D_2}} = \overrightarrow {{d_2}} \). Điều kiện cần và đủ để tứ giác \({A_2}{B_2}{C_2}{D_2}\) là hình bình hành là \(\overrightarrow {{a_2}} + \overrightarrow {{c_2}} = \overrightarrow {{b_2}} + \overrightarrow {{d_2}} \) (2)
Đặt \(\overrightarrow {OA} = \overrightarrow a ,\,\,\overrightarrow {OB} = \overrightarrow b ,\,\,\overrightarrow {OC} = \overrightarrow c ,\,\,\overrightarrow {OD} = \overrightarrow d \).
Ta có \({{A{A_1}} \over {A{A_2}}} = 3 \Rightarrow \overrightarrow {A{A_1}} = - 3\overrightarrow {A{A_2}} \)
\(\eqalign{
& \Leftrightarrow \overrightarrow {O{A_1}} - \overrightarrow {OA} = 3\left( {\overrightarrow {O{A_2}} - \overrightarrow {OA} } \right) \cr
& \Leftrightarrow \overrightarrow {{a_1}} - \overrightarrow a = - 3\left( {\overrightarrow {{a_2}} - \overrightarrow a } \right) \cr
& \Leftrightarrow \overrightarrow a = {1 \over 4}\left( {\overrightarrow {{a_1}} + 3\overrightarrow {{a_2}} } \right) \cr} \)
Advertisements (Quảng cáo)
Tương tự: \(\overrightarrow b = {1 \over 4}\left( {\overrightarrow {{b_1}} + 3\overrightarrow {{b_2}} } \right)\),
\(\overrightarrow c = {1 \over 4}\left( {\overrightarrow {{c_1}} + 3\overrightarrow {{c_2}} } \right),\overrightarrow {\,\,d} = {1 \over 4}\left( {\overrightarrow {{d_1}} + 3\overrightarrow {{d_2}} } \right)\).
Ta có: \(\overrightarrow a + \overrightarrow c = {1 \over 4}\left( {\overrightarrow {{a_1}} + 3\overrightarrow {{a_2}} } \right) + {1 \over 4}\left( {\overrightarrow {{c_1}} + 3\overrightarrow {{c_2}} } \right)\)
\(= {1 \over 4}\left( {\overrightarrow {{a_1}} + \overrightarrow {{c_1}} } \right) + {3 \over 4}\left( {\overrightarrow {{a_2}} + \overrightarrow {{c_2}} } \right)\)
Và:
\(\eqalign{
& \overrightarrow b + \overrightarrow d = {1 \over 4}\left( {\overrightarrow {{b_1}} + 3\overrightarrow {{b_2}} } \right) + {1 \over 4}\left( {\overrightarrow {{d_1}} + 3\overrightarrow {{d_2}} } \right) \cr
& = {1 \over 4}\left( {\overrightarrow {{b_1}} + \overrightarrow {{d_1}} } \right) + {3 \over 4}\left( {\overrightarrow {{b_2}} + \overrightarrow {{d_2}} } \right) \cr}\)
Từ (1) và (2) ta có \(\overrightarrow {{a_1}} + \overrightarrow {{c_1}} = \overrightarrow {{b_1}} + \overrightarrow {{d_1}} \) và \(\overrightarrow {{a_2}} + \overrightarrow {{c_2}} = \overrightarrow {{b_2}} + \overrightarrow {{d_2}} \) nên suy ra :
\(\overrightarrow a + \overrightarrow b + \overrightarrow c + \overrightarrow d \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {O{\rm{D}}} \)
⟺ tứ giác ABCD là hình bình hành.
