Cho tam giác ABC. Gọi \(\left( \alpha \right)\) là mặt phẳng vuông góc với đường thẳng CA tại A và \(\left( \beta \right)\) là mặt phẳng vuông góc với đường thẳng CB tại B. Chứng minh rằng hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) cắt nhau và giao tuyến d của chúng vuông góc với mặt phẳng (ABC).

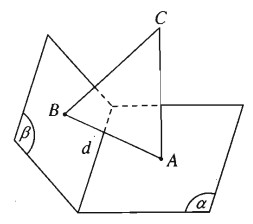
Hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) không thể trùng nhau vì nếu chúng trùng nhau thì từ một điểm C ta dựng được hai đường thẳng CA, CB cùng vuông góc với một mặt phẳng, điều đó là vô lí.
Mặt khác \(\left( \alpha \right)\) và \(\left( \beta \right)\) cũng không song song với nhau.
Advertisements (Quảng cáo)
Vì nếu \(\left( \alpha \right)\parallel \left( \beta \right)\), thì từ \(CB \bot \left( \beta \right)\) ta suy ra \(CB \bot \left( \alpha \right)\)
Như vậy từ một điểm C ta dựng được hai đường thẳng CA, CB cùng vuông góc với \(\left( \alpha \right)\), điều đó là vô lí.
Vậy \(\left( \alpha \right)\) và \(\left( \beta \right)\) là hai mặt phẳng không trùng nhau, không song song với nhau và chúng phải cắt nhau theo giao tuyến d, nghĩa là \(d = \left( \alpha \right) \cap \left( \beta \right)\)
\(\eqalign{
& \left\{ \matrix{
d \subset \left( \alpha \right) \hfill \cr
CA \bot \left( \alpha \right) \hfill \cr} \right. \Rightarrow CA \bot d\,\,\,\,\,\,\left( 1 \right) \cr
& \left\{ \matrix{
d \subset \left( \beta \right) \hfill \cr
CB \bot \left( \beta \right) \hfill \cr} \right. \Rightarrow CB \bot d\,\,\,\,\,\left( 2 \right) \cr} \)
Từ (1) và (2) suy ra \(d \bot \left( {ABC} \right)\).
